轨道动力响应的准静态计算

所谓结构动力分析的准静态计算,名义上是动力计算,而实质上则是静力计算。当由外荷载引起的结构本身的惯性力相对较小(与外力,反力相比),基本上可以忽略不计,而不予考虑时,则可基本上按静力分析的方法来进行,这就是准静态计算,而相应的外荷载则称为准静态荷载。

钢轨作为轨道结构的主要部件,其自振频率很高,高达1000 Hz。当轨道状态良好时,由机车车辆簧上及簧下部分质量的振动而产生的作用于轨道上的动荷载,其频率一般只有几十赫兹,不能激起钢轨的振动,而且碎石道床具有很高的阻尼消振作用,因此,在列车最后一个轮对过后基本测不到钢轨的振动在上节的静力计算中曾介绍过钢轨的弹性位移曲线。这个曲线随着轮载的前进而向前移动,称作进动波(Progressive Wave)。实测说明即使列车速度高达200 km/h,进动波形状与步行速度下的形状仍是一样的。这些都充分说明机车车辆作用于轨道的动荷载一般不能激发起钢轨的振动;高速条件下钢轨位移弹性曲线与按静载计算所得的弹性曲线基本上是相同的。这正是轨道强度的动力计算可以按准静态进行计算的理论和实验依据。

由于机车车辆的振动作用,作用在钢轨上的动荷载要大于静荷载,引起动力增值的主要因素是行车速度﹑钢轨偏载和列车通过曲线的横向力,分别用速度系数,偏载系数和横向水平力系数加以考虑,统称为荷载系数。

1 荷载系数

1.1速度系数

列车在直线区间轨道上运行时,由于轮轨之间的动力效应,导致作用在钢轨上的动轮载P_d要比静轮载大,其增量随行车速度的增加而增大。一般用速度系数α表示动载增量与静轮载之比P₀。

$$\alpha =\frac{P_d-P_0}{P_0}$$

则

$$P_d=(1+\alpha )P_0$$

速度系数α与轨道状态,机车类型等有关,可以通过大量试验确定。各国所采用的速度系数公式不尽相同，一般都是经验公式,大多与行车速度成线性或非线性关系。我国在行车速度ν≤200 km/h的线路上采用的计算式见表1,表中计算式用于计算轨底弯曲应力;当计算钢轨下沉及轨下基础各部件荷载及应力时,在表中基础上乘以0.75的折减系数。

表3 速度系数

对于速度在120~160 km/h时,动荷载表达式为P_d=(1＋α)(1＋α₁)P₀;对于速度在160～200 km/h时,动荷载表达式为P_d=(1＋α)(1＋α₁)(1＋α₂)P₀。

1.2 偏载系数

列车通过曲线时,由于存在未被平衡的超高(欠超高或过超高),产生偏载,使外轨或内轨轮载增加,其增量与静轮载的比值称为偏载系数,用β表示。

$$\beta =\frac{P_1-P_0}{P_0}$$

式中(公式5)

P₁——外轨(或内轨)上的轮载;

P₀——静轮载。

如图1所示,以欠超高为例推求β的计算公式。

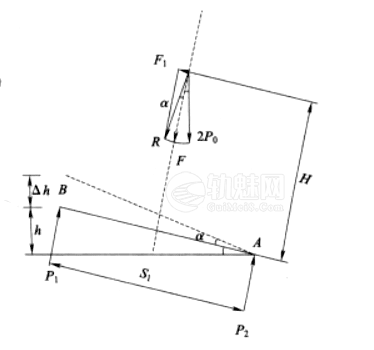
图1 欠超高情况

把合力R分解为垂直于轨面线的分力F和平行于轨面线的分力F₁,则由静力平衡条件∑M=0可得

$$P_1S_1=F\frac{S_1}{2}+F_1H$$

则（公式6）

$$P_1=\frac{F}{2}+F\frac{F_1}{S_1}$$

式中

H——车体重心高,货车一般取2.1～2.3 m;

S₁——左右钢轨中心线间距离,取1500 mm。因图中的α角度及δ角均很小,可取\(\cos\alpha =1，\cos\delta =1，\sin\alpha =\frac{\bigtriangleup h}{S_1},\sin\delta =\frac{h}{S_1}\)

由此得

$$F=2P_0,F_1=2P_O\frac{\bigtriangleup h}{S_1}$$

代入式(公式6)得

$$P_1=P_0+\frac{2P_0H\bigtriangleup h}{S^2_1}$$

代入式(公式5)得

$$\beta =\frac{2H\bigtriangleup h}{S^2_1}$$

可见β与稳定系数\(n=\frac{S^2_1}{2H\bigtriangleup h}\)互为倒数。

1.3 横向水平力系数

横向水平力系数ƒ是考虑横向水平力和偏心竖直力联合作用下,使钢轨承受横向水平弯曲及扭转,由此引起轨头及轨底的边缘弯曲应力增大而引入的系数,它等于钢轨底部外缘弯曲应力与中心应力的比值。

$$f=\frac{\sigma _1}{\frac{\sigma _1+\sigma _2}{2}}$$

式中,σ₁ ,σ₂分别为轨底外缘和内缘的弯曲应力;ƒ可以根据对不同机车类型及线路平面条件下σ₁ ,σ₂的大量实测资料,通过统计分析加以确定,见表2。仅在计算钢轨应力的动弯矩M_d中考虑ƒ值。

表2 横向水平力系数ƒ

2 准静态计算公式

2.1 钢轨竖向荷载

钢轨竖向荷载是指列车运行时车轮作用在钢轨上的竖向动轮载,用P_d表示。列车静止不动时,钢轨竖向荷载为静轮载,用P₀表示,它等于轴重的一半。列车运行时车辆轨道系统发生振动,加之偏载,风力作用等影响,动轮载要比静轮载大,产生动轮载增量(P_d一P₀)。影响动轮载的因素很多,计算也非常复杂,现有的设计方法主要考虑速度和未被平衡超高的影响,引进速度系数和偏载系数分别计算出动轮载增量,然后与静轮载迭加在一起得到动轮载。因此，钢轨竖向荷载是由静轮载、动轮载增量和偏轮载增量相加而成的动轮载P_d。

$$P_d=P_0(1+\alpha +\beta )(v\leq 120km/h)\\P_d=P_0(1+\alpha +\beta )(a+\alpha _1)(120km/h < v\leq 120km/h)\\P_d=P_0(1+\alpha +\beta )(a+\alpha _1)(a+\alpha _2)(160km/h < v\leq 200km/h)$$

2.2 动位移、动弯矩

要求得动位移y_d和动弯矩M_d,还要考虑动载增量影响。根据动轮载与静轮载的关系式(5.28),动位移和动弯矩分别为

当ν≤120 km/h时，

$$y_d=y_0(1+a+β)\\M_d=M_0(1+α+β)$$

当120 km/h<ν160 km/h 时，

$$y_d=y_0(1+α+β)(1+α_1)\\M_d=M_0(1+α+β)(1+α_1)$$

当160 km/h<ν200 km/h时，

$$y_d=y_0(1+α+β)(1+α_1)(1+α_2)\\M_d=M_0(1+α+β)(1+α_1)(1+α_2)$$

上述计算动位移、动弯矩和枕上动压力的方法叫准静态法,所得的计算公式叫做准静态公式。

文章来源：

郝瀛主编. 《铁道工程》[M]. 2000