圆曲线偏角法放样计算公式

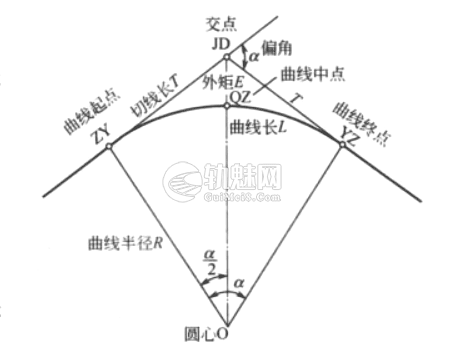
图1 圆曲线要素

1 测设数据的准备

如果已经转向角α和圆曲线半径R，圆曲线要素（图1）的计算公式如下:

切线长

$$T=R\cdot \tan\frac{\alpha}{2} $$

曲线长

$$L=\frac{\pi }{180}\alpha \cdot R$$

外矢距

$$E=R\cdot \left ( sec\frac{\alpha }{2}-1\right )$$

切曲差

$$q=2T-L$$

圆曲线主点桩号的计算及检核如下:󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄧󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

ZY桩号=JD桩号-T

QZ桩号=ZY桩号+L/2

YZ桩号=QZ桩号+L/2=ZY桩号+L

YZ桩号=JD桩号+T-q(检核)

2 主点测设

测设主点时，在转向点JD安置经纬仪，依次瞄准两切线方向,沿切线方向丈量切线长T,标定曲线的起点ZY和终点YZ。然后再照准ZY点，测设角(180°-a)/ 2，得分角线方向JD至QZ，沿此方向丈量外矢距E，即得曲中点QZ。

3 偏角法进行圆曲线的详细测设

偏角法（图2）是利用曲线起点（或终点）的切线与某一段弦长C_i来确定P_i点位置的一种方法。其特点是测点误差不积累。宜以QZ为界，将曲线分为两部分进行测设。(公式a)

$$\Delta _i=\frac{\varphi _i}{2}=\frac{l_i\cdot 90^\circ }{R\pi }\\c_i=2R\sin\Delta _i$$󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄧󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

式中，l_i是i至ZY点或YZ点的弧长φ_i为l_i所对应的圆心角。

图2 偏角法

步骤:首先按式(a)计算曲线上各桩点至ZY或YZ的弦长c_i及其与切线的偏角△_i，再分别架仪于ZY或YZ点，照准JD方向，使水平度盘读数为0°00’000″，然后拨角△_i，量边c_i。

需要注意的是，拨角分为正拨和反拨。正拨:偏角增加的方向与水平度盘读数增加方向一致，即顺时针方向旋转拨角;反拨:偏角增加的方向与水平度盘读数增加方向相反，即逆时针方向旋转拨角。若切线方向的水平度盘读数为0°00’00″，正拨:度盘读数=偏角值;反拨:度盘读数=360°一偏角值。󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄧󠄢󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

4 注意事项

偏角法测设时，拉距是从前一曲线点开始，必须以对应的弦长为半径画圆弧，与视线方向相交，获得当前测设的曲线点。注意偏角的拨转方向及水平度盘读数;

文章来源：

崔立鲁主编. 《工程测量实验指导》[M]. 2016