1.木枕顶面承压应力
木枕顶面承压应力为
$$\sigma _s=\frac{R_d}{F}\leq \left [\sigma _s \right ] $$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
式中
σs——木枕横纹承压动应力(MPa);
F——轨底或垫板与木枕的接触面积(mm2) ;󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
Rd——钢轨动压力(N);
〔σs〕——木材横纹允许承压应力,松木取1.4 MPa,杉木取10.4 MPa,桦木取3.9 MPa,桉木取4.2MPa。
2.混凝土轨枕弯矩
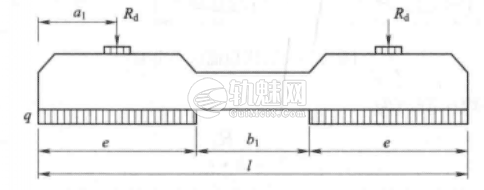
图1 轨下截面正弯矩计算图示
计算轨枕弯矩时,通常把它视为支承在弹性基础上的短梁,分别取最不利支承方式。检算轨下截面正弯矩Mg,采用图1所示的道床支承方式,假定轨枕中间部分完全掏空,可得Mg的检算公式为
$$M_g=K_s\left ( \frac{\alpha ^2_1}{2e}-\frac{b’}{8}\right ) R_d\leq [M_g]$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
式中
a1——荷载作用点至枕端距离,取a=50 cm;
e——一股钢轨下,轨枕的全支承长度,取e=95 cm;󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
b——轨下衬垫宽度,一般取轨底宽(cm);󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
Ks——轨枕设计系数,暂定为1;
〔Mg〕——轨下截面允许弯矩,与轨枕类型有关,Ⅰ型枕可取为11.9 kN ·m,Ⅱ型枕可取为13.3 kN ·m,Ⅲ型枕可取为18 kN·m。
检算中间截面负弯矩Mc时,采用图2所示的道床支承方式,即轨枕中部为部分支承,道床支承反力取全支承的¾时。

图2 跨中截面负弯矩计算图示
图2 跨中截面负弯矩计算图示Mc的检算公式为
$$M_c=-K_s\frac{3l^2+4e^2-8a_1e-12a_1l}{4(3l+2e)}R_d\leq [M_c]$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
式中
l——轨枕长度(cm);
〔Mc〕——中间截面允许负弯矩,与轨枕类型有关,Ⅰ型枕可取8.8 kN·m,Ⅱ型枕可取10.5 kN·m,对于Ⅲ型枕,其支承型式为全面支承Mc,的检算公式为
$$M_c=-K_s\frac{L-4a_1}{4}R_d\leq [M_c]$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
Ⅲ型枕中间截面的允许负弯矩可取为14 kN·m。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
〔Mg〕,〔Mc〕可由轨下断面和中间断面未开裂极限弯矩除以相应的安全系数求得。木枕有足够的抗弯强度,一般不进行此项检算。
文章来源:
易思蓉主编《铁道工程》[M]. 2009



