曲线上任意点矢距的计算
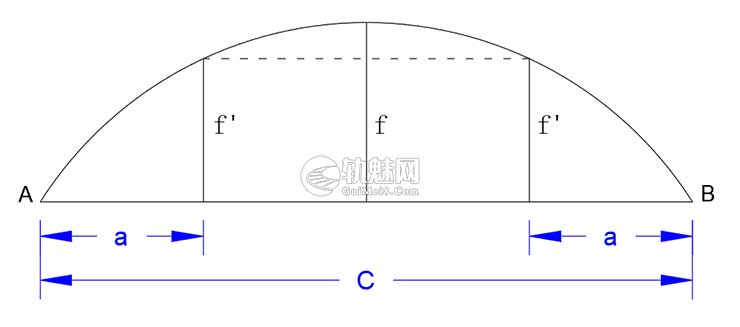
如上图所示,设弦长AB=C,如上所述,󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$f=\frac{C^2}{8R}$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
距AB弦始终点为a的任意点的矢距f’,等于正矢f减去以(C-2a)为弦的正矢,即󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$${f}’=\frac{C^2}{8R}-\frac{\left (C-2a \right )^2}{8R}\\
=\frac{4aC-4a^2}{8R}=\frac{4a(C-a)}{8R}\\
=\frac{a(C-a)}{2R}$$
如\(a=\frac{1}{8}C\),则󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$${f}’_{1/8}=\left [ \frac{4C}{8}\left ( C-\frac{C}{8}\right )\right ]\div 8R\\
=\frac{4}{8}\times \frac{7}{8}\times \frac{C^2}{8R}=\frac{7}{16}f$$
如\(a=\frac{1}{4}C\),则󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$${f}’_{1/4}=\left [4\times \frac{C}{4}\left ( C-\frac{C}{4}\right )\right ]\div 8R\\
=\frac{3}{4}\times \frac{C^2}{8R}=\frac{3}{4}f=\frac{12}{16}f$$
如\(a=\frac{3}{8}C\),则󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$${f}’_{3/8}=\left [4\times \frac{3C}{8}\left ( C-\frac{3C}{8}\right )\right ]\div 8R\\
=\frac{3}{8}\times \frac{5}{2}\times \frac{C^2}{8R}=\frac{15}{16}f$$
计算例题:
例:曲线半径300m,弦长30m,求3m处矢距?
根据上式$${f}’=\frac{a(C-a)}{2R}$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
得:$${f}’=\frac{3\times(30-3)}{2\times300}=0.135m=135mm$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮



