铁路曲线计划正矢点布置方式及计算方法

1 前言

我国目前逐年新增的运营线路长度，传统的铁路线路维修方式日益被机械化维修所取代，尤其是大型养路机械的广泛使用，对曲线正矢维修养护，提出更高的要求。曲线养护关键在于合理的对曲线正矢和超高进行布置，现就常用的铁路曲线计划正矢布置方式和计算方法进行归纳，供现场参考使用。

2 常用的曲线正矢布置方式

目前我国还没有一种设计规范和行业标准硬性规定铁路曲线正矢测量点布点方法，各个铁路集团公司及工务段都根据各自作业习惯和传统采用多种不同的曲线正矢布点方法。其中较为常见的有测点对称布点、曲线一端的头或尾落在测点上的布置法、曲线头尾与测点重合布置法、任意布置法、增加副矢等五种，现分别归纳如下：

2.1 曲线对称布点法

以QZ 点为中心分别向两侧的ZH、HZ 对称等距布点，按里程增加依次编号，该方法又分为QZ 点与测点重合和QZ 点与测点不重合两种。

曲线对称布点可简化曲线计划正矢计算，计算正矢时可只计算曲线一端，另一端对称填写，计算时间短，是工务部门用得最多的布置方法。󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄡󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

2.2 曲线一端头或尾落在测点上的布置法

以ZH 或HZ 点为起点向曲线另一端等距布点，并按里程增加或减少方向依次编号。本方法虽然其始端可以用同测点重合时特殊公式计算计划正矢，但因为绝大多数曲线全长不是10m 整倍数，其另一端缓和曲线上每个正矢与始端不对称，必须另外计算，部分工务部门使用。

2.3 曲线头尾与测点重合布置法

ZH、HY、YH、HZ 都落在测点上，两端测点分别从ZH、HZ 向曲中点QZ 等距分布，至QZ 点不足两测点间距S 时不再设桩，且将不足的余量放在圆曲线中间。

本方法ZH、HZ 与测量点重合，优点是计划正矢、曲线加宽和超高顺坡起终点明确，但因为绝大多数曲线长不是10m 整倍数，在圆曲线中间有一处两测点间距不足S 的桩，测点间距不等长，计划正矢变为计划矢距，计算公式稍复杂，部分工务部门使用。󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄡󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

2.4 任意布置法

指ZH 或HZ 点至前后桩的距离为任意长度（要求小于等于测点间距），向曲线另一端布桩，既不对称，测点也不与曲线头尾重合，此种情况新开通线路很少采用，但在既有曲线整正重新计算计划正矢时经常用到。

2.5 既有布点上加密测点法

在以上四种布置桩方法基础上，在10m 测点（假设原测点间距为10m）中间再增加测点，点间距由原10m变为5m，测量时每隔5m 移动一次弦绳，检查方法不变。如测点间采用20m 弦线，原测点(1，2，3，……，n)为一组，加密点(1′，2′，3′．……n′) 为另一组测量正矢, 测量结果为两组实测正矢数据，加密测点的目的在于进一步保证曲线的圆顺，但现场测量和计算工作量大，被大多数工务部门采用。

3 计划正矢计算方法

目前曲线计划正矢计算方法通常有绳正法、坐标法、偏角法，各自的理论不同优缺点也不同，但坐标法计算出的计划正矢的结果是精度最高，适应性最好，可计算不等间距测点的矢距，下面就坐标法计算进行介绍。

3.1 建立坐标系及曲线五段方程

我国常用铁路曲线由两端的切直线、缓和曲线及中间的圆曲线五个线元组成，现建立以ZH（HZ）点为坐标原点，始（终）切线为X 轴的坐标系，形成线路五段方程，以S 里程为自变量，在ZH 处里程取值为0，则HY点为L₀₁，YH点为L − L₀₂，HZ为L，各段参数方程可参考相关资料，证明从略：

第一段方程：- ∞～ZH( 第一切线,S 取值范围:- ∞～0 之间)

x = S， y =0， β =0󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄡󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

第二段方程：ZH ～HY( 第一缓和曲线):

$$x=S-\frac{S^5}{40\times R \times l^2_{01}},y=\frac{S^3}{6\times R \times l_{01}}-\frac{S^7}{336\times R^3 \times l_{01}^3},\beta =\frac{S^2}{2 \times R \times l_{01}}$$󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄡󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

第三段方程：HY ～YH( 圆曲线)

任意点的切线方向，直接求导数，󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄡󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

$$x=R \times \sin(\beta )+m_1,y=R \times \left ( 1- \cos\left (\beta \right ) \right )+P_1,\beta=\frac{l^2_{01}}{2 \times l_{01} \times R}+\frac{\left ( S-l_{01}\right )^2}{R}$$󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄡󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

第四段方程：YH ～HZ( 第二缓和曲线)

$$x=T_1+T_2\times \left ( \frac{\left ( L-S\right )^3}{6 \times R \times l_{01}}-\frac{\left ( L-S\right )^7}{336 \times R^3 \times l^3_{01}}\right )\times \sin (a) -\left ( L-S\right )\times \frac{1-(L-S)^4}{40\times \left ( l_{02}\times R\right )^2}\times \cos (a)$$󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄡󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

$$y=T_2\times \sin(a) – (L-S) + \frac{1-\left ( L-S\right )^4}{40 \times \left (l_{02}\times R \right )^2}\times \sin(a)+\left ( \frac{\left ( L-S\right )^3}{6\times R\times l_{02}}-\frac{\left ( L-S\right )^7}{336 \times R^3 \times l^3_{02}}\right )\times \cos(a)$$󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄡󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

$$\beta =a-\frac{\left ( L-S\right )^2}{2\times l_{02}\times R}$$󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄡󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

第五段方程：HZ ～+ ∞( 第二切线，自变量S 为从ZH 点开始至计算点的线长.)

$$x=T_1+T_2\times \cos(a)+(S-L)\times \cos(a)\\y=T_2\times \sin(a)+(S-L)\times \sin(a)\\\beta =a=\frac{L_{01}+L_{02}}{2\times R}+\frac{L-L_{01}-L_{02}}{R}$$󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄡󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

公式说明：

a——曲线转角；L——曲线全长；S——ZH 点至计算点间的长度；\(l_{01}、l_{02}\) ——缓和曲线长；R——圆半径。󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄡󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

$$曲线总转角：a=\frac{L_{01}+L_{02}}{2\times R}+\frac{L-L_{01}-L_{02}}{R} \quad 测点切线方位角：\beta (rad)$$󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄡󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

$$曲线切线长度：T_1=\frac{R+P_2}{\sin(a)}-\frac{R+P_1}{\tan(a)}+m_1 \quad T_2=\frac{R+P_1}{\sin(a)}-\frac{R+P_2}{\tan(a)}+m_2$$󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄡󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

$$缓和曲线内移距：P_1=\frac{l^2_{01}}{24\times R}-\frac{l^4_{01}}{2688\times R^3} \quad P_2=\frac{l^2_{02}}{24\times R}-\frac{l^4_{02}}{2688\times R^3}$$󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄡󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

$$缓和曲线切垂距：m_1=\frac{l_{01}}{2}-\frac{l_{01}^3}{240\times R^2}+\frac{l_{01}^5}{34560\times R^4} \quad m_2=\frac{l_{02}}{2}-\frac{l_{02}^3}{240\times R^2}+\frac{l_{02}^5}{34560\times R^4}$$󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄡󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

3.2 计算各点的计划正矢

根据铁路曲线五段坐标方程，计算出各测点坐标，以点至直线的距离数学公式，推导出正矢公式（公式-1）及矢距公式（公式-2）

已知\(A(X_{i-1}，Y_{i-1}) 、 B(X_{i}，Y_{i}) 、 C(X_{i+1}，Y_{i+1})\) 三点坐标，求中间B 点至直线AC 的距离BD，如图1。󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄡󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

3.2.1 当测点间距相等时，

$$f_1\sqrt{\left ( x_i-\frac{x_{i+1}+x_{i-1}}{2}\right )^2+\left ( y_i-\frac{y_{i+1}+y_{i-1}}{2}\right )^2} \qquad (公式-1)$$󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄡󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

3.2.2 当测点间距不相等时，󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄡󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

$$f_i=\frac{\left | \frac{y_{i+1}+y_{i-1}}{x_{i+1}+x_{i-1}}\times x_i-y_i+y_{i-1}-x_{i-1}\times \frac{y_{i+1}+y_{i-1}}{x_{i+1}+x_{i-1}}\right |}{\sqrt{\frac{\left (y_{i+1}+y_{i-1} \right )^2}{\left (x_{i+1}+x_{i-1} \right )^2}+1}} \qquad (公式-2)$$󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄡󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

3.3 曲线加宽及超高计算：

根据规范要求，确定缓和曲线地段加宽及超高顺坡率起终点，计算各桩对应的加宽及超高值（计算过程从略）。

4 计划正矢布置及计算实例

以上五种布置方法，各有特点，现以“曲线头尾与测点重合布置法”为例进行计算。

已知曲线要素： R=800.7175（曲线上股工作边）， l₀₁=70，l₀₂=70， L = 272.972，测点间距10m，以曲线头尾与测点重合布置法为例进行计算，即从ZH、HZ 点向QZ 点对称布桩。

4.1 测点布置：

中间零弦长度=272.972（曲线全长）-10.0（测点间距）*27（倍数）=2.972m，2.972m<10m，直接采用，其中ZH=1#，HY=8#，YH=22#，HZ=29# 桩，零弦端点桩号为15#、16# 桩点，测点布置方式如图2。

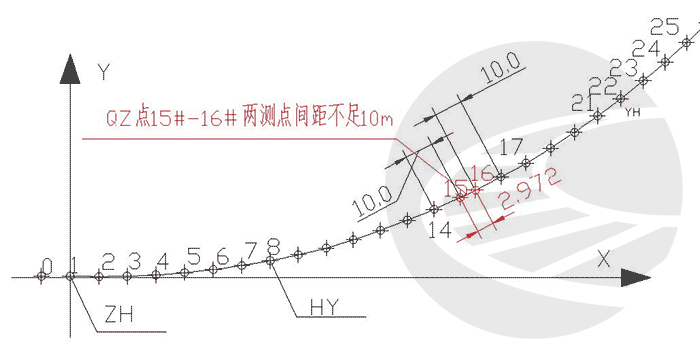
4.2 测点计划正矢：

根据“曲线五段方程”公式计算出各测点坐标，根据（公式1）及公式（公式2）计算计划正矢或矢距，计算成果如表1。

序号	始缓长L1	终缓长L2	半径R	曲全长LY	始切长T1	终切长T2	曲线偏角a
1	70	70	800.7175	272.972	137.063	137.063	14°31′25.55″
测点间距	ZH至第1测点距离m	曲线超高(mm)	曲线加宽(mm)	ZH上股相对里程(m)	HY上股相对里程(m)	YH上股相对里程(m)	HZ上股相对里程(m)	行别/曲线号
10	0	20	0	0	70	202.972	272.972
桩号	正矢mm	X,Y坐标	超高mm	加宽mm	相对里程(m)	测点间距(m)	线形	曲线桩
0	0	-10,0	0	0	-10	0	始直
1	1.5	0,0	0	0	0	10	始直	ZH:0+0
2	8.9	10,.003	2.9	0	10	10	始缓
3	17.8	20,.024	5.7	0	20	10	始缓
4	26.8	30,.08	8.6	0	30	10	始缓
5	35.7	39.999,.19	11.4	0	40	10	始缓
6	44.6	49.998,.372	14.3	0	50	10	始缓
7	53.5	59.994,.642	17.1	0	60	10	始缓
8	61	69.987,1.02	20	0	70	10	始缓	HY:8+0
9	62.4	79.974,1.519	20	0	80	10	圆曲
10	62.4	89.955,2.143	20	0	90	10	圆曲
11	62.4	99.926,2.892	20	0	100	10	圆曲
12	62.4	109.888,3.765	20	0	110	10	圆曲
13	62.4	119.838,4.762	20	0	120	10	圆曲
14	62.4	129.775,5.884	20	0	130	10	圆曲	QZ:14+6.485
15	18.6	139.697,7.13	20	0	140	10	圆曲
16	18.6	142.643,7.524	20	0	142.972	2.972	圆曲
17	62.4	152.543,8.93	20	0	152.972	10	圆曲
18	62.4	162.426,10.46	20	0	162.972	10	圆曲
19	62.4	172.288,12.113	20	0	172.972	10	圆曲
20	62.4	182.129,13.889	20	0	182.972	10	圆曲
21	62.4	191.947,15.787	20	0	192.972	10	圆曲
22	61	201.74,17.809	20	0	202.972	10	圆曲	YH:22+0
23	53.5	211.509,19.949	17.1	0	212.972	10	终缓
24	44.6	221.253,22.194	14.3	0	222.972	10	终缓
25	35.7	230.978,24.526	11.4	0	232.972	10	终缓
26	26.8	240.685,26.927	8.6	0	242.972	10	终缓
27	17.8	250.379,29.38	5.7	0	252.972	10	终缓
28	8.9	260.065,31.868	2.9	0	262.972	10	终缓
29	1.5	269.746,34.373	0	0	272.972	10	终直	HZ:29+0
30	0	279.427,36.881	0	0	282.972	10	终直

5 结束语

上述五种曲线计划正矢布置方式，各有优缺点，可根据需要进行选择使用。计算方法统一采用坐标法，可精确计算出各测点的计划正矢或矢距，本方法计算过程较复杂，人工计算工作量大且易出错，若通过编写计算机程序进行计算，可极大提高工作效率和计算准确度，为满足铁路曲线养护的品质化、精细化和标准化要求打下坚实的基础。

文章来源：

原文名称：铁路曲线计划正矢布置方式及计算方法综述󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄡󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

作者信息：廖显军(中国铁路南宁局集团有限公司)󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄡󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

期刊信息：铁道建设企业管理 第24期󠄐󠄹󠅀󠄪󠄢󠄡󠄦󠄞󠄧󠄣󠄞󠄢󠄡󠄦󠄞󠄡󠄡󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮