[图解]铁路不对称型抛物线竖曲线计算

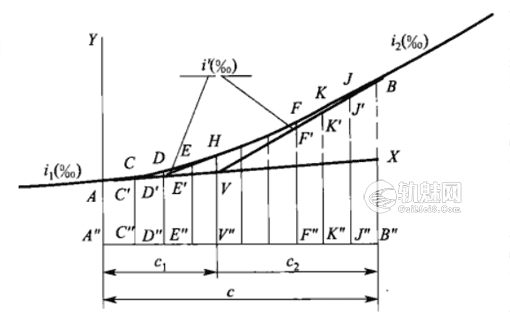
图1 不对称抛物线竖曲线示意

图中:

i₁——切线 AV的坡度(‰);

i₂——切线BV的坡度( ‰) ;

V——变坡点;

C——竖曲线长度(m),ADHFB的投影;C₁=ADH；

C₂=HFB,但C₁≠C₂≠C/2;

D’——AV的中点,A”D”=D”V”=C₁/2;

F’——BV 的中点,B”F”=F”V”=C₂/2;

i’——D’F’线的坡度(‰)。󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄨󠄨󠄞󠄢󠄥󠄢󠄞󠄡󠄠󠄠󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

从图中分析,大的竖曲线ADHFB实际上是由i₁与i’形成的ADH和由i’与i₂形成的HFB两部分竖曲线所组成。其长度不一,即不对称,应分别进行计算。

由图可得

$${i}’=\frac{C_1i_1+C_2i_2}{C_1+C_2}=\frac{C_1i_1+C_2i_2}{C}$$󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄨󠄨󠄞󠄢󠄥󠄢󠄞󠄡󠄠󠄠󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

变坡率有所不同:

ADH部分

$$\gamma _1=\frac{20}{C_1}({i}’-i_1)$$󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄨󠄨󠄞󠄢󠄥󠄢󠄞󠄡󠄠󠄠󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

HFB 部分

$$\gamma _2=\frac{20}{C_2}(i_2-{i}’)$$󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄨󠄨󠄞󠄢󠄥󠄢󠄞󠄡󠄠󠄠󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

其任意点纵距计算:

ADH部分

$$y_1=\frac{\gamma _1\cdot x^2_1}{40000}$$󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄨󠄨󠄞󠄢󠄥󠄢󠄞󠄡󠄠󠄠󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

HFB 部分

$$y_2=\frac{\gamma _2\cdot x^2_2}{40000} $$󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄨󠄨󠄞󠄢󠄥󠄢󠄞󠄡󠄠󠄠󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

中央点纵距计算:

ADHFB内中央点纵距为

$$y_{VH}=\frac{\gamma _1\cdot C^2_1}{40000} $$󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄨󠄨󠄞󠄢󠄥󠄢󠄞󠄡󠄠󠄠󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

ADH部分中点纵距为

$$y_{DD’}=\frac{C}{8} (i’-i)$$󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄨󠄨󠄞󠄢󠄥󠄢󠄞󠄡󠄠󠄠󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

HFB部分中央点纵距为

$$y_{FF’}=\frac{C_2}{8} (i_2-i’)$$󠄐󠄹󠅀󠄪󠄡󠄨󠄞󠄡󠄨󠄨󠄞󠄢󠄥󠄢󠄞󠄡󠄠󠄠󠄬󠅒󠅢󠄟󠄮󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮

文章来源：

 陈知辉编著. 《铁路曲线轨道》[M]. 2009