曲线上某一测点向外或向内有一拨量,则其相邻两测点的正矢将相应减小或增大此拨量的一半。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
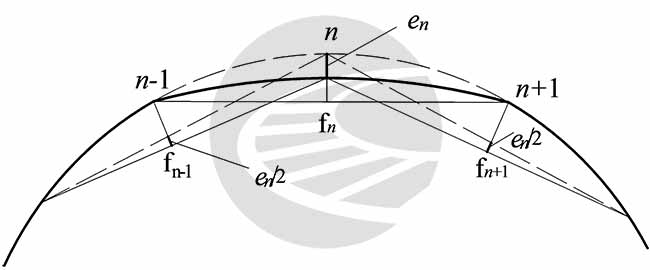
如图所示,当\(n\)点向外的拨量为\(e_n\)时,其前后两测点的正矢\(f_{n+1}\)及\(f_{n-1}\)将各减少\(\frac{e_n}{2}\)。反之,其前后两测点的正矢将各增加\(\frac{e_n}{2}\)。因此,若\(n-1\)点的拨量为\(e_{n+1}\),\(n\)点的拨量为\(e_n\), \(n+1\)点的拨量为\(e_{n+1}\),则\(n\)点拨量后的正矢为:󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$f^\prime _n=f_n+e_n-\left ( \frac{f_{n+1}+f_{n-1}}{2} \right ) $$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
式中:
\(f^\prime _n\)———\(n\)点处拨后正矢󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
\(f_n\)———\(n\)点处现场正矢󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
\(e_n\) ———\(n\)点处拨动量󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
\(f_{n-1}\) ———\(n-1\)点前点拨动量󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
\(f_{n+1}\) ———\(n+1\)点后点拨动量󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
简易拨道法是利用前后测点正矢相互影响关系,计算拨道量的,这种方法简单,算出的拨道量较小。它的主要缺点是控制不住曲线头、尾。经常用这种方法计算拨道,将使曲线头尾往往变更位置,以致使超高、轨距加宽递减范围的曲线正矢与标准不符。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
介绍这种计算拨道法的目,主要是这种方法适合于曲线圆度较好,仅个别有误差的情况,特别是对曲线的个别小调整,用此法更为方便。但是,绝不能长期使用,以免造成曲线“鹅头”现象。现将简易拨道法举例说明如下表所示.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
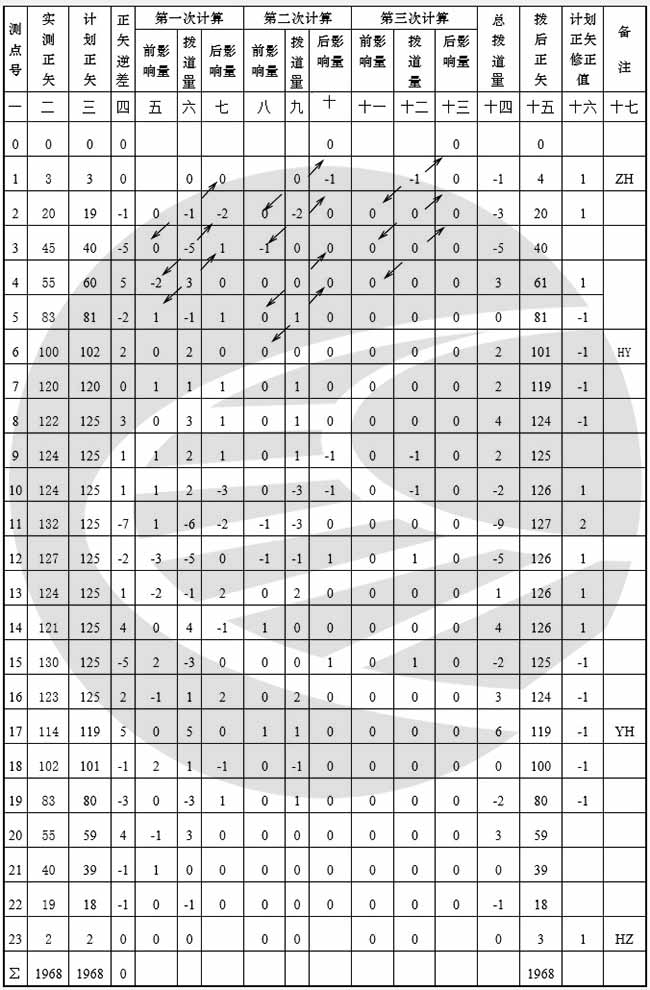
第4列的正矢逆差与以前的绳正法有所不同,正矢逆差=计划正矢-实测正矢󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
第6列是第一次计算拨道量:拨道量的计算方法是根据正矢逆差与前影响量之代数和为该点的拨道量,得出的拨道量又对相邻两点各影响一半,符号相同的方法,分为前影响量和后影响量。例如e3=df3+第三点的前影响量=-5+0= -5。
第三点的拨动量-5又以半数,符号相同分给第二点的后影响量-2,分给第四点的前影响量-2(0.5不计数 ,所以前后影响量应为-2.5均取-2)传递类推之。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
第二次计算(9列)拨道量:第一次计算后,如果后影响量有数值 ,并大于1者,则须再进行第二次计算。进行第二次计算时,第一次的后影响量和第二次的前影响量之代数和,即为第二次拨道量,同理将第二次的拨道量再以相邻二点各一半,符号相同的方法,分给前测点的后影响量和后测点的前影响量。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
按上述方法,经过一次、二次或多次计算,直到后影响量全为“0”或有数值不超过1时为止。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
第十列总拨道量的计算方法是:总拨道量为各次计算拨道量之和。列如第7点总的拨道量=1+1+0=2.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
最后第十五列的拨后正矢的计算是根据拨动一点,影响相邻测点各动半数的原理,校对每一测点的拨后正矢是否与计划正矢相符。具体做法,先将各点总拨道量数值,加上括号移入校对栏内,把该数值分为二,符号相反,一半分给前一点,另一半分给后一点,再将实测正矢移入这一栏,取代数 和即得出拨后正矢。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
最后拨后正矢与计划正矢相对照,如拨后正矢与计划正矢差在2毫米之内,其原因是取含“0.5”所致,不算误差。如超过2毫米时,则说明计算有误。因查其原因改正之。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮



