轨道结构具有边运营边维修的特点,曲线位置变化一直是影响列车运营舒适度、安全性的重要因素。铁路工作者一直伴随测绘技术的不断发展研究相应算法。从绳正法、偏角法、坐标法直到轨检小车测量,测量的手段和效率不断提升,计算结果的可靠性也更为准确。对于大量的既有线路而言,采用坐标法进行线路曲线测量具有易选取置镜点位置、整体测量对线路运营干扰小且工作效率比较高的特点而得以广泛应用。目前基于坐标法进行曲线测量和整正的方法主要存在 2 方面的问题:󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
一是对初始半径及缓和曲线长的计算,刘文涛等采用圆曲线段最小二乘法求得初始半径及缓和曲线长,但在数据处理过程中圆曲线段长度难以确定且计算数据较大。候茂盛采用圆曲线段 3 点数据计算初始半径及缓和曲线长,在圆曲线段较长时缺乏代表性。二是在拨道量优化算法的设计,任少伟等通过最小拨道量求出最优半径及缓和曲线长,覃乃轩等采用半径和缓和曲线长的不同组合求出最小拨道量来确定最优半径及缓长,算法虽然减少了对曲线的扰动但在计算过程中拨正前后曲线长度变化引起的无缝线路实际锁定轨温变化,不利于养护维修工作。本文根据实测线路坐标,采用几何重心法计算初始半径及缓和曲线长。结合最小曲线扰动和轨道长度不变性原则,利用初始曲线长,计算最优半径、缓长及拨道量。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
1 基于坐标测量的曲线整正算法基本思路
1.1 坐标法曲线整正过程
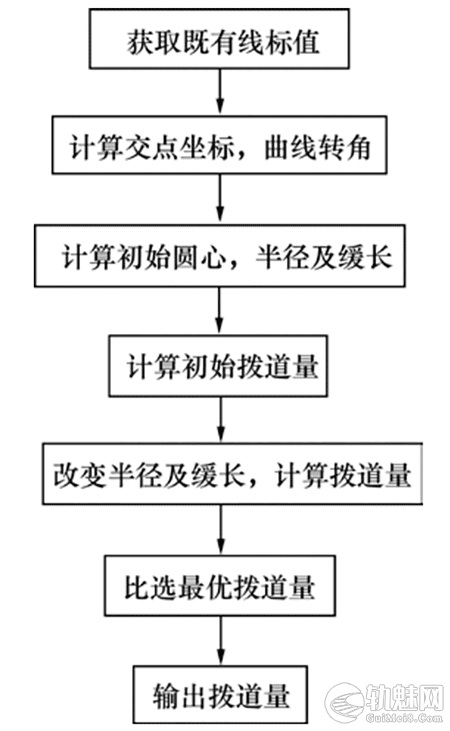
曲线整正问题的实质就是如何利用现有的实测数据获取最为可靠的初始半径及缓和曲线长度,并借助优化算法实现其最优的半径及缓和曲线长度组合,获取满意的线形。基于坐标测量的曲线整正算法基本思路如图 1 所示。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
从流程图中可以看出,曲线整正计算的关键环节主要包括曲线偏角、初始半径、初始缓和曲线长度计算,优化算法设计等方面。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
1.2 铁路既有线整正计算的基本要求
1) 铁路既有线整正时整正前后必须满足:󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
① 曲线转角值不变;
② 整正前后轨道长度保持不变;
③ 坐标测量的起点和终点在曲线外的直线上,起点和终点的整正拨距为 0,保证线路两端的位置是固定不变以确定直线的方向不变;󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
2) 拨道量计算结果要求:在满足设计的各条件要求下各测点整正的拨道量平方和为最小值。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
3) 特殊位置既有线整正要求:在实际的铁路既有线上整正过程中,当遇到整正既有曲线的控制点时,例如桥梁、隧道、涵洞、等大型建筑物,这些控制点的整正拨道量值要小于规定的数值。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
4) 半径与缓和曲线的要求:优化拨道量的过程中半径的取值要符合《铁路线路设计规范》(TB11009—2017)表 5.4.1 中规定的最小曲线半径值。缓和曲线要符合《铁路线路设计规范》表 5.4.3-1中规定的缓和曲线最小长度。采用的曲线半径在困难条件下,可采用规定范围内 10 m的整倍数。特殊困难条件下按曲线半径进整值进行取值。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
2 关键算法设计
确定一条完整的铁路曲线位置需要确定线路的曲线转角α,交点坐标(XJD,YJD),曲线半径R,缓和曲线长度l01和l02。
2.1 常用计算初始半径及圆心方法
目前常用的初始半径与圆心坐标计算方法主要有 3 点法与最小二乘法。3 点法是取圆曲线范围内的中间 3 个测点坐标求出初始半径与圆心坐标,当圆曲线段线段较长时,缺乏代表性。并且当中间3 点的测点受列车影响较大时,计算结果缺乏可靠性。最小二乘法求初始半径与圆心坐标是通过圆曲线段所有测点经过最小化误差的平方和寻找数据的最佳值。首先通过 n 个测点 3 点定圆的方式求出n-2 个圆心与半径,做出半径变化图或者做出曲率变化图,通过变化图中半径或曲率变化较大的点近似确定圆缓点与缓圆点确定圆曲线范围。在确定半径或曲率变化较大的点时,变化量没有统一的定义,圆曲线范围难以确定。并且最小二乘法求初始半径与圆心坐标计算量较大。
2.2 几何重心法计算初始圆心及半径
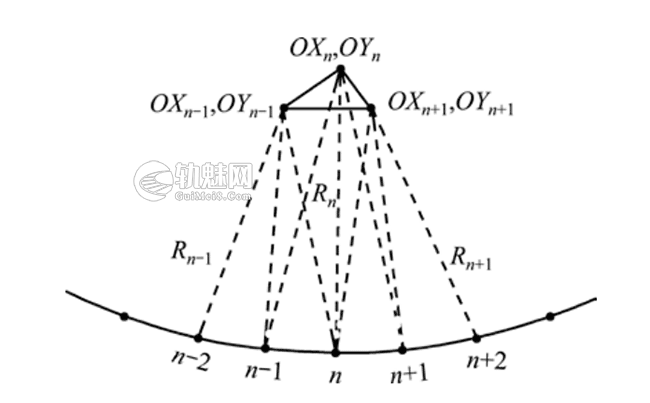
按照 3 点定圆的方法,从曲线中心第n点向两侧分别选取相邻的 2 个点位,共计 5 个点。利用n-2,n-1 和n ,3 个点位确定可行半径Rn-1及圆心坐标(OXn-1,OYn-1),利用n-1,n和n+1 3 个点位确定可行半径Rn及圆心坐标(OXn,OYn),利用n,n+1 和n+2 3 个点位确定可行半径Rn+1及圆心坐标(OXn+1,OYn+1),如图 2 所示。
则初始半径Rs:
Rs=(Rn-1+Rn+Rn+1)/3 (公式1)
可将相应的(OXn-1,OYn-1),(OXn,OYn),(OXn+1,OYn+1)3 点所构成的三角形的重心坐标作为初始圆心坐标,计算公式为:
OX=(OXn-1+OXn+OXn+1)/3 (公式2)
OY=(OYn-1+OYn+OYn+1)/3 (公式3)
对于较长的曲线可以向两侧选取较多的点位参与初始半径计算,利用多边形几何重心法求解相应的初始圆心坐标及半径。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
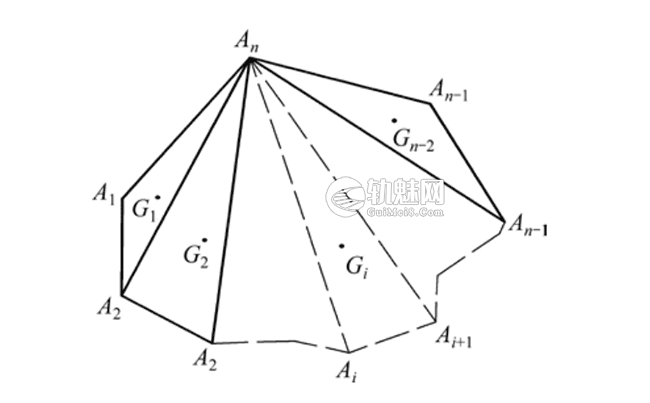
多边形几何重心计算公式:较长的曲线向两侧选取较多的点位,根据 3 点成圆的方法,确定n个圆心坐标,由这n个坐标可以构成n边形。如图 3 所示,以A1,A2,…,An为顶点各坐标为(X1,Y1),(X2,Y2),…,(Xn,Yn),可以把n边形分成n-2 个三角形,各三角形重心为G1(x1,y1),G2(x2,y2),…,Gn-2(xn-2,yn-2),面积分别为σ1,σ2,…,σn-2。则多边形几何重心如下所示。
$$x=\frac{\sum^{n-2}_{i=1}\sigma _i x_i}{S_{A1,A2,L,An}}\qquad (公式4)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$y=\frac{\sum^{n-2}_{i=1}\sigma _i y_i}{S_{A1,A2,L,An}}\qquad (公式5)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
式中:\(x_i=\frac{X_n+X_j+X_{j+1}}{3},y_i=\frac{Y_n+Y_j+Y_{j+1}}{3}\)󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$\sigma _i=\frac{1}{2}\times \begin{vmatrix}
X_n &Y_n & 1\\
X_i &Y_i &1 \\
X_{i+1}& Y_{i+1} & 1
\end{vmatrix}$$
$$S_{A1,A2,L,An}=\frac{1}{2}\left \{ \begin{vmatrix}
X_1&Y_1 \\
X_2&Y_2
\end{vmatrix}+\begin{vmatrix}
X_2 & Y_2\\
X_3 &Y_3
\end{vmatrix} +,L,+\begin{vmatrix}
X_n &Y_n \\
X_1 & Y_1
\end{vmatrix}\right \}$$
通过几何重心法与传统的 3 点法和最小二乘法求初始的半径结合实例对比可以得出,几何重心法计算简单,计算结果符合实际。如表 1 所示。
表 1 半径计算结果对比
| 测区 | 3 点法 | 几何重心法 | 最小二乘法 | |||
| 所需 测点 |
半径/m | 所需 测点 |
半径/m | 所需 测点 |
半径/m | |
| 1 | 3 | 605.6 | 5 | 593.2 | 8 | 605.6 |
| 2 | 3 | 583.3 | 6 | 602.7 | 14 | 601.2 |
| 3 | 3 | 810.9 | 5 | 806.4 | 14 | 805.4 |
| 4 | 3 | 589.6 | 5 | 603.1 | 11 | 606.4 |
| 5 | 3 | 1038.3 | 6 | 1 002.1 | 25 | 1002.4 |
| 6 | 3 | 764.7 | 5 | 795.6 | 15 | 802.6 |
| 7 | 3 | 778.6 | 5 | 806.6 | 19 | 806.9 |
| 8 | 3 | 806.5 | 6 | 801.4 | 18 | 797.9 |
| 9 | 3 | 609.3 | 6 | 599.7 | 19 | 603.3 |
2.3 初始缓和曲线长度计算
由图 4 可以看出,初始圆心到 2 条切线的距离D1和D2理论上是初始半径与前后缓和曲线对应的内移距之和:
$$D_1=R_S+P_1=\frac{l^2_{01}}{24R_s}\qquad (公式6)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$D_2=R_S+P_2=\frac{l^2_{02}}{24R_s}\qquad (公式7)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
根据求解的P1和P2,选择初始缓和曲线长度:
$$l_{01}=\sqrt{24R\times P_1}\qquad (公式8)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$l_{02}=\sqrt{24R\times P_2}\qquad (公式9)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
当l01和l02相差不超过 10 m时,取二者平均值作为初始缓和曲线长度,按照等长缓和曲线进行计算。
当l01和l02相差超过 10 m时,各自取整,按照不等长缓和曲线进行计算。
2.4 最优半径及缓和曲线长度确定
目前常用的优化方法是组合法,以不同半径及缓长组合成多组(R, l01, l02)组合,通过计算机辅助计算求出最优的拨道量。此类优化方法虽能求出拨道量最优值但拨正前后曲线长度变化引起的无缝线路实际锁定轨温变化,不利于养护维修工作,基于这种情况以既有线初始半径及缓和曲线长下的曲线长L为约束条件对拨道量进行优化,按缓和曲线长的设置情况其优化可分为以下 2 种情况。
1) 对称优化:即前后缓和曲线长度相等,此时优化参数有 2 个:缓长l0和半径R。半径步长ΔR以曲线转角和步长关系进行取值,按正负 2 个方向取n组值。由式(10)可推导出等长缓和曲线长下半径与缓长关系式(11),计算各R±ΔR下对应的l0,并将l0取整为10 m的整倍数,得到不同R与l0的组合,计算各组拨道量。以初始R与l0所对应的初始拨道量为参考值,以目标函数最小值,比选出最优的半径、缓长及拨道量。
$$L=(a-\beta _{01}-\beta _{02}\times R+l_{01}+l_{02})\qquad (公式10)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$l_0=L-a\times R\qquad (公式11)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
2) 非对称优化:即前后缓和曲线长度不相等,此时优化参数有 3 个:缓长l01,l02和半径R。半径步长ΔR以曲线转角和步长关系进行取值,按正负 2个方向取n组值。由式(10)可推导出不等长缓和曲线长下半径与缓长关系式(12),固定l01,计算各R±ΔR下对应的l02,并将l02取整为 10 m的整倍数,改变l01重复上述步骤,得到不同R与l01和l02的组合,计算各组拨道量。以初始R与l0所对应的初始拨道量为参考值,以目标函数最小值,比选出最优的半径、缓长及拨道量。
$$l_{02}=2L-2aR-l_{01}\qquad (公式12)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
曲线拨道量目标函数:
$$f(x)=\sum_{n}^{i=1}\bigtriangleup ^2_i\qquad (公式13)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
曲线拨道量目标函数可以验证曲线整正结果是否良好,以各测点(即各里程点)的拨道量的平方和为计算结果。
通过组合法优化拨道量与曲线长约束优化拨道量结合实例得到的最优值看出,组合法拨道量最优值略好于曲线约束法,但曲线约束法优化拨道量对轨道曲线段长度的影响较小,可以减少无缝线路的养护维修工作,更好的满足曲线整正要求,如表2 所示。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
表2 优化方法计算对比
| 测区 | 优化方法 | 目标函数/m² | 曲线段长度变化/m |
| 1 | 曲线约束法 | 0.022 | 1.77 |
| 组合法 | 0.0115 | -15.51 | |
| 2 | 曲线约束法 | 0.0593 | 3.08 |
| 组合法 | 0.0341 | -8.3 | |
| 3 | 曲线约束法 | 0.0267 | 0 |
| 组合法 | 0.023 | -4.63 |
3 算法实现
3.1 现场数据采集
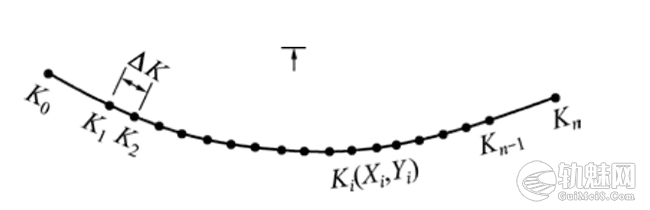
由于铁路既有线整正是在铁路轨道丈量完成的条件下进行的,所以本算法首先要求完成轨道里程的丈量工作,曲线地段每 20 m,曲线外侧明显的直线地段测量至少 2 个点,如图 5 中的K0,K1以及Kn-1,Kn以确定直线方向。剩余直线段每 20 m为一个测点。测量过程中,置镜在轨道外,建立相对坐标系,得到各测点坐标Xi,Yi,及确定始点里程K0和计算步距ΔK,如图 5 所示。
3.2 数据计算
根据本文所设计的算法,结合铁路既有线实测数据(表 5 中原 X 与 Y 值),通过计算机程序语言编制相应的程序,使计算更加快速准确。
1) 交点坐标及曲线转角计算如图 4 所示,按照实测直线段点位A和B的坐标计算直线AB的方位角A1及直线方程,按照实测直线段点位C,D的坐标计算直线CD的方位角A2及直线方程,则曲线转角:
$$a=A_2-A_1\qquad (公式14)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
利用推求的直线方程可以求解曲线交点坐标(XJD,YJD),如表 3 所示。
表 3 曲线转角及交点坐标
| 名称 | 曲线转角 A | 交点坐标 X | 交点坐标 Y |
| 值 | -0.342 | 8 000.717 | 5 004.177 |
2) 初始圆心、半径及缓长根据本文所设计的算法,求出初始半径与缓和曲线长,如表 4 所示。
表 4 既有线初始圆心、半径及缓和曲线长
| 名称 | 初始圆心 X | 初始圆心 Y | 初始半径 R | 初始l01 | 初始l02 |
| 值/m | 7 421.462 | 4 806.112 | 600 | 50 | 50 |
3) 设计坐标及拨道量计算
根据选取的初始半径Rs,缓和曲线长度l01,l02,考虑交点坐标(XJD,YJD),偏角α,初始里程LC等因素,采用文献 16 的算法可以简洁计算出曲线上各点理论坐标。
可以利用实测坐标和理论坐标之间的距离作为拨道量,并根据其与圆心之间的距离判断拨道方向。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
4) 曲线整正优化
根据本文所设计的算法,结合铁路既有线实测数据确定最优半径为 600 m 缓和曲线长为 50 m 时拨道量值为最优值,曲线拨后坐标和拨道量如表 5所示,最优目标函数值为 0.0295。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
表 5 拨道量及整正前后坐标值
| 里程/m | 原 X 值/m | 原 Y 值/m | 拨后 X 值/m | 拨后 Y 值/m | 拨道量/m |
| 63 640 | 7 923.576 | 5 145.272 | 7 923.576 | 5 145.272 | 0.000 |
| 63 660 | 7 933.153 | 5 127.755 | 7 933.153 | 5 127.755 | 0.000 |
| 63 680 | 7 942.761 | 5 110.204 | 7 942.762 | 5 110.174 | -0.030 |
| 63 700 | 7 952.239 | 5 092.627 | 7 952.253 | 5 092.569 | 0.060 |
| 63 720 | 7 961.394 | 5 074.843 | 7 961.414 | 5 074.791 | 0.056 |
| 63 740 | 7 970.015 | 5 056.742 | 7 970.032 | 5 056.744 | 0.017 |
| 63 760 | 7 978.042 | 5 038.372 | 7 978.044 | 5 038.420 | 0.048 |
| 63 780 | 7 985.420 | 5 019.824 | 7 985.441 | 5 019.839 | 0.026 |
| 63 800 | 7 992.192 | 5 001.000 | 7 992.214 | 5 001.022 | 0.031 |
| 63 820 | 7 998.343 | 4 981.980 | 7 998.356 | 4 981.990 | 0.016 |
| 63 840 | 8 003.860 | 4 962.709 | 8 003.861 | 4 962.763 | 0.054 |
| 63 860 | 8 008.722 | 4 943.326 | 8 008.722 | 4 943.364 | 0.038 |
| 63 880 | 8 012.942 | 4 923.763 | 8 012.934 | 4 923.813 | 0.051 |
| 63 900 | 8 016.573 | 4 904.065 | 8 016.554 | 4 904.114 | 0.061 |
| 63 920 | 8 019.841 | 4 884.363 | 8 019.815 | 4 884.412 | 0.055 |
| 63 940 | 8 022.990 | 4 864.612 | 8 022.972 | 4 864.629 | -0.024 |
| 63 960 | 8 026.117 | 4 844.894 | 8 026.122 | 4 844.878 | -0.016 |
| 63 980 | 8 029.272 | 4 825.128 | 8 029.272 | 4 825.128 | 0.000 |
| 64 100 | 8 048.165 | 4 706.665 | 8 048.165 | 4 706.665 | 0.000 |
4 适用范围
本文关于既有线曲线整正的算法在《铁路线路设计规范》(TB11009—2017)中客货共线铁路、重载铁路所要求的半径及缓和曲线长的情况下进行设计,所设计的算法也即适用于客货共线铁路、重载铁路的整正设计。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
5 结论
1) 通过实测数据计算采用几何重心法所求得的初始半径、缓长及圆心计算简单准确,计算结果符合工程实际。采用的优化算法可以减少无缝线路的养护维修工作,更好的满足曲线整正要求。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
2) 坐标法在对既有线进行曲线整正计算中操作灵活,理论严密,计算简洁。并且能直观体现半径及缓和曲线长改变对坐标值与拨道量的影响。结合计算机语言辅助计算可以使计算过程更加快速,准确。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
文章来源:
作者 : 王博[1] 韩峰[2]
作者单位 :兰州交通大学 测绘与地理信息学院,甘肃 兰州,730070;兰州交通大学 土木工程学院,甘肃 兰州,730070
刊 名: 铁道科学与工程学报 ISTICPKU
原文名称:基于坐标测量的既有曲线整正算法设计与实现





感谢分享