坐标法曲线整正计算方法探讨

铁路既有线经过长期运营后，原有的轨道线形将发生较大变化。特别是曲线部分，线形不再有初期那么平顺，线路不平顺直接影响到旅客乘车的舒适性和列车运行的安全。因此，铁路既有线需要定期进行复测，为线路大修、改造及养护维修提供准确的线路技术参数，恢复线路平顺度。传统的既有线平面测量方法主要有偏角法、矢距法和绳正法，它们的计算原理均基于渐伸线原理，但是渐伸线原理比较复杂，人工计算工作量相当大，并且是近似计算，计算精度低，运用现行的渐伸线法求得的既有半径、缓和曲线长度往往与现状不符，产生较大拨道量，成为既有线勘测设计中的一个突出问题。因此，探讨如何采用坐标法对铁路既有曲线进行整正计算的方法，据有十分重要的现实意义。

1 外业坐标数据采集要求

随着现代测量技术和计算机技术的快速发展，特别是全站仪和全球卫星定位技术GPS的普及和应用，为坐标法复测既有曲线提供了有利的条件，使能整体确定铁路曲线几何状态、优化设计半径、合理选配曲线元素、受行车干扰小的坐标法测量成为现实。外业坐标数据采集要求：

1）采用自由设站法。用三脚架或轨道小车固定全站仪棱镜或GPS RTK移动站进行线路中心线坐标采集。

2）坐标点采集间隔。当使用全站仪时，建议直线地段按20 m左右、曲线地段按10 m左右间距采集；当使用GPS-RTK时，建议不管是直线还是曲线，全部按不大于5 m间距自动采集，以提高拟合精度。

3）为便于现场里程放样和掌握控制点的拨道量，需要同时对线路特征点（如道岔中心、进站信号机、桥梁中心、大中桥的桥台胸墙和台尾、隧道进出口、涵渠中心、立交桥中心、平交道口、公里标、百米标、曲线五大桩等）进行坐标采集。

4）为确保曲线两端切线方向准确，直线地段测量长度一般不应短于200 m，当夹直线较短时，相邻的两曲线应联测联算，并确保夹直线方向不变。

5）当使用全站仪一站无法观测完一个曲线时，按导线方法增设转点，并满足导线测量精度要求。

2 测点里程及拨量计算原理

2.1 曲线相关参数计算

假设曲线始终端直线方程y=k₁x+b₁和y=k₂x+b₂已经确定，曲线半径为R，始终端缓和曲线长分别为L_s1和L_s2，那么，曲线在整个平面中的位置就固定下来（如图1所示）。根据两直线方程，分别求得它们的交点坐标（x_jd，y_jd），始终端切线方位角A₁和A₂，曲线转角a和转向系数i（左转
i=1，右转i=-1）；根据缓和曲线计算公式及平面几何关系，分别计算出曲线的其它参数，包括切线长T₁、T2，切垂距m₁、m2，内移距P₁、P₂，缓和曲线角β₁、β₂，外距E、圆心坐标（x_o，y_o）、曲线主要点坐标及其方位角和里程等（ZH里程可通过指定的测点引出）。以上参数的计算，相关教科书中均有计算公式，在这里就不再一一列式计算。

图1 缓和曲线计算图

2.2 测点属性判断

由于测点的里程和拨量在直线段、缓和曲线段和圆曲线段采用计算方法不同，因此，计算前首先要判断各测点的属性（即测点所在的线元）。本文始端切线、始端缓和曲线、圆曲线、终端缓和曲线、终端切线的线元分别用Z₁、H₁、Y、H₂、Z₂表示。

2.2.1 切向量定义

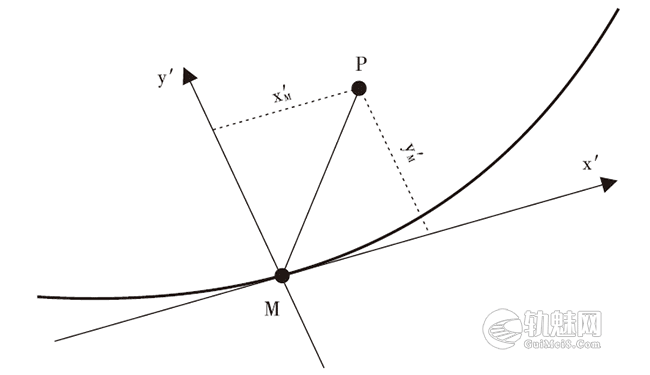
设P为设计中线外一测点，坐标为（x，y），M为设计曲线上一点，坐标为（x_M，y_M），M点对应的切线方位角为A_M，P点相对于M点的切向量和法向量分别用x′_M、y′_M表示（见图2）。

图2 P点相对于M点向量计算图

根据平面几何关系可得：

$$\left.\begin{matrix}
{x}’_M=S_{MP}\times \cos\left ( A_{MP} -A_{M}\right )\\
{y}’_M=S_{MP}\times \sin\left ( A_{MP} -A_{M}\right )
\end{matrix}\right\}\qquad (1)$$

式中SMP为MP直线的距离，AMP为MP直线的方位角。

2.2.2 测点属性判断方法

首先按式（1）顺序计算P 点相对于ZH、HY、YH、HZ 点的切向量x′_ZH、x′_HY、x′_YH、x′_HZ，然后根据P点相对于相临分界点切向量的正负号来判断P点在分界点处法线的哪一侧，从而判断P点属于哪个线元范围，具体判断方法详见测点属性判断流程图（图3）。

图3 测点属性判断流程图

2.3 里程及拨量计算

2.3.1 直线段

直线段任意测点的里程等于ZH（HZ）里程加上其相对于ZH（HZ）点的切向量x′_ZH（x′_HZ）：

$$\left.\begin{matrix}
K_{Z1}=K_{ZH}-{x}’_{ZH}\\
K_{Z2}=K_{HZ}-{x}’_{HZ}
\end{matrix}\right\}\qquad (2)$$

直线段任意测点的拨量等于其相对于ZH（HZ）点的法向量y′_ZH（y′_HZ）：

$$\left.\begin{matrix}
D_{Z1}={y}’_{ZH}\\
D_{Z2}={y}’_{HZ}
\end{matrix}\right\}\qquad (3)$$

当拨量值为正值时表示测点偏离设计中心线左侧（指顺里程方向），为负值时表示测点偏离设计中心线右侧，以下缓和曲线和圆曲线段均相同。

2.3.2 缓和曲线段

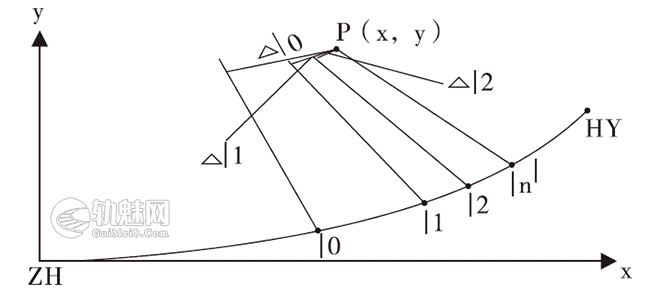
设P 为始端缓和曲线外一测点，其全局坐标转换成ZH坐标系坐标为（x，y），对应的缓和曲线参数为l（见图4），l 值可按式（4）迭代计算求得：

\(l_{n+1}=l_n+\bigtriangleup _{ln}\qquad (4)\)

式中：\(\bigtriangleup _{ln}\)=0，1，2，3，…，初值\(l_0=x\)。

\(\bigtriangleup l _n\)为P点到缓长l_n对应法线的距离，按式（5）计算：

$$\bigtriangleup l _n=\cos\left ( A_{nP}-i\times \beta _n \right )\times \sqrt{\left ( x+x_n \right )^2+\left ( y+y_n \right )^2 }\qquad (5)$$

式中：A_np为ln缓长对应的中桩点到P点的方位角；

i为转向系数；

（x_n，y_n）和β_n分别为缓长l_n对应的中桩坐标（ZH坐标系）和缓和曲线角。

当Δl_n≥0.0001m时停止迭代，这时P点对应的缓长l 就等于l_n+1。对于铁路缓和曲线，由于缓和曲线角较小，Δl_n值收敛较快，一般只需1～3次迭代计算就能满足毫米级精度要求。求得后，P点对应的里程就可按式（6）计算：

$$K_{H1}=K_{ZH}+l\qquad (6)$$

P点的拨量按式（7）计算：

$$D_{HZ}=\sin\left ( A_{lp} -i-\beta _1\right )\times \sqrt{\left ( x-x_l \right )^2+\left ( y-y_l \right )^2}\qquad (7)$$

式中：A_lP为缓长l对应的中桩点到P点的方位角；

（x₁，y₁）和β₁分别为缓长l 对应的中桩坐标（ZH坐标系）和缓和曲线角。

同理，可计算终端缓和曲线段的里程和拨量。

图4 缓和曲线长度计算图

2.3.3 圆曲线段

圆曲线段各测点的里程等于HY点里程加上从HY点到测点所对应的圆弧长：

$$K_Y=K_{HY}+a_pR\qquad (8)$$

式中a_P为从HY点到测点P所对应的切线转角（即圆心角），即a_P=A_OP-A_OHY。

各测点的拨量等于圆曲线半径减去测点到圆心点的距离：

$$D_Y=i \times \left ( R-\sqrt{\left ( x-x_0 \right )^2+\left ( y-y_0 \right )^2}\right )\qquad (9)$$

3 线路参数拟合

3.1 直线拟合

直线方程可表示为y=kx+b，式中k为直线斜率；b为y轴上的截距。根据该式，始终端夹直线参数可以分别采用直线上2个距离较远的点直接确定，也可采用直线上多个测点通过最小二乘法直线拟合来确定。关于直线拟合的具体方法在许多文献中均有介绍，不再赘述。

3.2 曲线拟合

目前文献中介绍的一般都是先计算曲线上各测点的曲率，然后根据曲率变化情况选择圆曲线段的坐标点用最小二乘法原理进行曲线半径和圆心拟合，再根据拟合出的曲线半径和圆心坐标反求缓和曲线长度，最后计算拨道量。这种拟合方法存在一个缺点就是缓和曲线和曲线头部分的线路未能完全按最小二乘法原理参与整体拟合，因此拟合出的曲线参数不是最优的，特别是缓和曲线较长、圆曲线较短时更为明显。

本文介绍的曲线参数拟合原理仍是最小二乘法原理，但采用的方法是半径和缓长逐次逼近整体优化方法，利用计算机编程技术优选出最佳曲线半径和缓和曲线长，并使得各测点拨量平方和最小，同时半径和缓长满足规范要求。根据铁路缓和曲线的特点，不外乎有以下3种情况。

3.2.1 缓长优化半径

根据给定的缓长对半径进行优选，并使得各测点的拨量平方和最小，这时优化参数只有1个，即半径R。我们不妨根据一个固定的缓长，按不同的半径，分别计算出各测点的拨量平方和，并在坐标系中绘制半径-拨量曲线图，从这个图不难看出该曲线是个开口向上的二次抛物曲线，其拨量平方和必定有最小值，因此采用了逼近法对半径进行优选。具体优化方法：首先以半径步长为1 000 m，半径范围从100～13 000 m，分别和已知缓长配对进行拨量计算，并找出拨量平方和（包含选定的直线段、缓和曲线段、圆曲线段的拨量）最小的半径，然后再以上次半径步长的1/10作为本次半径步长，以上次最小拨量平方和的半径加减上次半径步长的1/2作为本次半径取值范围，分别和已知缓长配对进行拨量计算，并找出最小拨量平方和的半径，如此循环计算，直至半径步长等于0.1 m时所对应的最小拨量平方和的半径就是最优半径。

3.2.2 对称优化

按对称缓和曲线对缓长和半径同步进行优化，这时优化参数有2个，即Ls和R。具体优化方法：初步给定一个缓长，按缓长优化半径方法求得最小拨量平方和，再以初步缓长加10 m优化半径求得的最小拨量平方和，两者比较，如果后者小于前者，则继续按10 m步长递增缓长进行优化半径，直至最小拨量平方和不再减小为止，最后所得到的缓长和半径就是最优的；反之，如果后者大于前者，则以反方向递减缓长进行优选。

注意在优化过程中应对最小圆曲线段长度加以限制（一般不小于20 m），否则求出的前后缓和曲线可能会在曲线上发生重叠现象。

3.2.3 非对称优化

按非对称缓和曲线对缓长和半径同步进行优化，这时优化参数有3个，即Ls1、Ls2和R。鉴于铁路曲线一般设计之初都是以对称缓和曲线进行设计的，即使后期运营缓长发生改变，其变化范围也不会太大，所以在优化缓和曲线时，可以先按对称优化方法对缓长和半径进行优化，得到的缓长作为曲线始终端缓长的初值，然后按初值固定一端缓长，按对称优化方法优化另一端缓长和半径，再以优化得到的缓长作为固定端，再按对称优化方法优化另一端缓长和半径，这样，反复交换优化得到的缓长作为固定端进行优化另一端缓长，直到始终端缓长均不再变化为止，最后优化得到的缓长和半径就是最优的。

4 结束语

按以上方法对黔桂线0 km曲线进行计算，该曲线共有165个数据点（GPS-RTK测量），按对称优化进行计算用时1 s，按最为复杂的非对称优化进行计算用时2 s，其计算结果快速准确。实例计算证明本方法具有外业测量操作简单、安全高效，内业计算数学模式理论严密、优化程度较高、结果快速准确的优点。主要表现一是外业测量只需采集线路中心线坐标，测量效率成倍提高。二是对测点属性的判断是通过计算测点相对于相临线元分界点切向量的正负符号来判断的，从而避免了由于测量偶然误差造成的误判。三是曲线参数拟合采用整体优化法，整个曲线上的所有数据点均参与拟合计算，确保拟合出的曲线参数最优，线形最切合实际，拨道工作量最小。

文章来源:

作者 姓名： 覃乃轩[1] 孙和金[2]

作者单位 ：柳南铁路有限责任公司；南宁铁路局工务处,广西南宁,530003

刊名： 铁道运营技术