既有线拨道量与线路伸缩量的关系

1 前言

目前线路曲线整正拨道量与线路伸缩量关系都是根据曲线换轨空搭头理论计算原理^[1]，通过近似地计算出来，公式如下：文章源自轨魅网轨魅网-https://www.guimei8.com/7647.html

$$\bigtriangleup l=\frac{e_{平均}\times l}{R}$$文章源自轨魅网轨魅网-https://www.guimei8.com/7647.html

\(\bigtriangleup l\)———拨道后曲线的伸长或缩短量文章源自轨魅网轨魅网-https://www.guimei8.com/7647.html

\(e_{平均}\)———平均拨量，等于各测点拨量代数和除以测点数文章源自轨魅网轨魅网-https://www.guimei8.com/7647.html

\( l\)———曲线的拨道长度文章源自轨魅网轨魅网-https://www.guimei8.com/7647.html

本公式是以圆曲线缩短量计算的原理，以拨移量代替两股钢轨中心距，但公式中并不反映缓和曲线、直线地段及部分曲线如何计算，所以存在诸多缺陷，适用性受到严格限制。在曲线拨道整正中，常出现不均匀的拨量量，容易造成钢轨内部应力集中，特别是在对拨量有严格要求的无缝线路地段，现有的计算方法远远不能满足现场工作的需要。文章源自轨魅网轨魅网-https://www.guimei8.com/7647.html

现根据标准曲线弦弧长度差的原理，能比较精确地还原既有线路长度，通过设计线路与既有线路长度之差，计算出拨后线路伸缩量，为线路现场作业提供可靠的理论依据。文章源自轨魅网轨魅网-https://www.guimei8.com/7647.html

2 线路拨道量与线路伸缩量的关系文章源自轨魅网轨魅网-https://www.guimei8.com/7647.html

拨后线路伸缩量直线与曲线地段计算方法不致，下面分别介绍。文章源自轨魅网轨魅网-https://www.guimei8.com/7647.html

2.1 直线地段既有线长度计算文章源自轨魅网轨魅网-https://www.guimei8.com/7647.html

2.1.1  根据实测坐标，建立统一方程文章源自轨魅网轨魅网-https://www.guimei8.com/7647.html

以坐标法为例进行拨后线路伸缩量的计算方法，首先选取曲线两端切线上任意两测点A,B确定切线方向，以始端第一测点A为坐标原点，两点连线为横坐标建立新坐标系，将原坐标系的测点通过平移旋转为新坐标系X-O-Y的坐标。如图1所示，A和B为直线两个固定点，以A为坐标原点，AB为横坐标。文章源自轨魅网轨魅网-https://www.guimei8.com/7647.html

图1 设计直线与既有线位置关系图

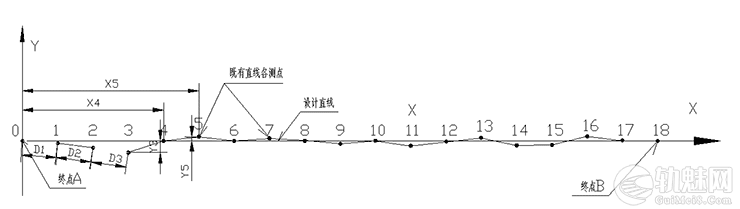
设A点坐标为横坐标X_A，纵坐标Y_A；B点坐标为X_B,Y_B，中间各点的坐标为X_i，Y_i，则长大直线A B的方位角为：\(\beta _{AB}=arctg\left ( \frac{Y_B-Y_A}{X_B-X_A}\right )=arctg\left ( \frac{\Delta Y}{\Delta X}\right )\)，平移旋转坐标后各测点坐标为：文章源自轨魅网轨魅网-https://www.guimei8.com/7647.html

$$X^{'}_i=(X_i-X_A)\times \cos(\beta _{AB})+(Y_i-Y_A)\times \sin (\beta _{AB})\qquad(公式1)\\Y^{'}_i=(Y_i-Y_A)\times \cos(\beta _{AB})-(X_i-X_A)\times \sin (\beta _{AB})\qquad(公式2)$$文章源自轨魅网轨魅网-https://www.guimei8.com/7647.html

2.1.2  直线拨后线路缩短量计算文章源自轨魅网轨魅网-https://www.guimei8.com/7647.html

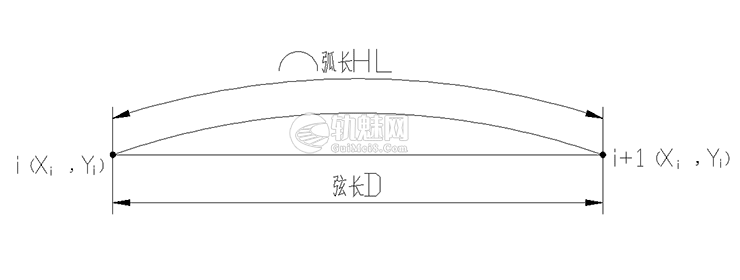
如图2所示，根据既有各测点坐标，两点间弦长为：文章源自轨魅网轨魅网-https://www.guimei8.com/7647.html

$$D_i=\sqrt{(x_{i+1}-x_i)^2+(y_{i+1}-y_i)^2}$$文章源自轨魅网轨魅网-https://www.guimei8.com/7647.html

图2 设计直线与既有线位置关系图

各弦长累计等于既有线的长度：文章源自轨魅网轨魅网-https://www.guimei8.com/7647.html

$$L_i=\sum ^n_1D_i=\sum ^n_{i=1}\sqrt{(x_{i+1}-x_i)^2+(y_{i+1}-y_i)^2}\qquad(公式3)$$文章源自轨魅网轨魅网-https://www.guimei8.com/7647.html

拨后直线线路某点累计缩短量E_i=设计线路长度X_s-既有线路长度L_i，即文章源自轨魅网轨魅网-https://www.guimei8.com/7647.html

$$E_i=X_s-L_i=X_i-\sum ^n_{i=1}\sqrt{(x_{i+1}-x_i)^2+(y_{i+1}-y_i)^2}\qquad(公式4)$$

X_s——自直线线路起点至某计算点的线路里程（长度），等于横坐标值。

2.2 曲线地段既有线长度计算

曲线优化拟合后得出设计曲线半径R、缓和曲线l₀和曲线转角α与既有曲线要素已相当接近，如图3所示，既有测i点整正后，沿法线方向拨至理论位置i′，同理测点i+1点拨至i+1′，设计线路i′～i+1′段弧长可根据设计里程差而得，在统一坐标系X-O-Y下坐标为x_i，y_i，x_i+1'，y_i+1'。

图3 设计曲线与既有线位置关系图

设既有线某两测点，i及i+1点的横纵坐标为x_i，y_i，x_i+1'，y_i+1'，则弦长\(D_i=\sqrt{(x_{i+1}-x_i)^2+(y_{i+1}-y_i)^2}\)，设该段设计线路弧长为HL_i'，则弧弦差

$$\Delta L_{i'}=HL_{i'}-D_{i'}-\sqrt{(x_{i+1'}-x_{i'})^2+(y_{i+1'}-y_{i'})^2}\qquad(公式5)$$

图4 设计线弧长与弦长关系图

经过优化后的设计线与既有线的曲率想当接近，即\(\rho _j\approx \rho _s\)，故所有对应的设计标准曲线弦弧差与既有曲线弦弧差相当，即\(E_j\approx E_s\)，则既有曲线还原后的长度L_j公式为：

$$L_j=\sum ^n_{i=1}\sqrt{(x_{i+1}-x_{i})^2+(y_{i+1}-y_{i})^2}+\sum ^n_{i'=1'}\left (HL_{i'}- \sqrt{(x_{i+1'}-x_{i'})^2+(y_{i+1'}-y_{i'})^2}\right )\qquad(公式6)$$

2.3  某段线路拨后缩短量计算公式

综合以上直线及曲线地段的既有线长度还原公式，可知既有线某测点拨后线路伸缩量等于设计线路长度减去既有线长度，推导公式如下 ：

设某计算点设计线路长度L_s，既有线长度L_j，则某段线路拨后缩短量如下：

$$\Delta E_i=L_j-L_s=\left ( \sum ^n_{i=1}\sqrt{(x_{i+1}-x_{i})^2+(y_{i+1}-y_{i})^2}+\sum ^n_{i'=1'}\left (HL_{i'}- \sqrt{(x_{i+1'}-x_{i'})^2+(y_{i+1'}-y_{i'})^2}\right )\right )-L_s\qquad(公式7)$$

\(\Delta E_i\)———某点拨后线路伸缩量

\(\sum ^n_{i=1}\sqrt{(x_{i+1}-x_{i})^2+(y_{i+1}-y_{i})^2}\)———既有线路弦长累计

\(\sum ^n_{i'=1'}\left (HL_{i'}- \sqrt{(x_{i+1'}-x_{i'})^2+(y_{i+1'}-y_{i'})^2}\right )\)———设计线路弧弦差累计

\(L_s\)——设计线路长度

这就是既有线拨后线路伸缩量计算公式。

本方法是根据坐标法整正拨量原理^[2]计算，如图3，流动坐标系X'-O'-Y'沿着设计线路中心线移动，如既有测点在流动坐标系中横坐标值|x'|≤0.5mm，则认为既有线某测点落在纵轴上，y'值即为拨量，设计线路对应则产生一测点，设计里程为L_s，如此类推，既有线有N个测点，则设计线路产生相应的N个测点，线路分成N-1段，将既有线路、设计线路各分段长度累计之差，即为拨后线路伸缩量。

3  计算实例

以某文献坐标法整正曲线 ^[3]为例，现采用与文献优化相同的曲线要素进行整正，即以第1#、16#、37#和50#桩为控制点确定切线方向，以18#、19#桩连线且距18#桩8.6301m的点为坐标原点，1#、16#桩连线方向为横坐标建立新坐标系，设计相对里程以ZH=0(m)，1#、16#、37#和50#测点相对里程如图5所示。

图5 设计曲线与既有曲线位置关系图

既有线及设计线长度及拨后线路伸缩量表2、表3。

表1  优化后曲线要素表

表2  既有线及设计线长度计算表

表3  拨后线路伸缩量表

由表1-3可知，拨后线路总伸缩量为-0.1mm，累计缩短量最大值位于位于曲线地段的28#～33#桩，为-1.1mm，曲线地段向上挑线路伸长，反之则缩短，而直线地段伸缩量几乎没有随拨量变化而变化，符合了线路拨道量与伸缩量的普遍规律。

上诸表中19#～36#为曲线地段，曲线长度L=321.139 m，缓和曲线长度l₀=50mm，圆曲线长度l=321.139-100=211.139m，半径拨R=3151.01 m，拨量代数和为83.4mm，平均拨量\(e_{平均}=\frac{84.3}{18}=4.6mm\)，根据传统的伸缩量公式\(\Delta l=\frac{e_{平均}\times l}{R}=\frac{4.6\times 211.139}{3151.01}=0.32mm\)，与本方法计算的结果-0.1mm相差约0.4mm，传统计算方法严格来说并不准确，是因为它是按近似计算造成的，同样的拨道量，直线、缓和曲线及圆曲线地段单位长度拨后伸缩量并不相等。

5 结束语

通过标准曲线弦弧长度差还原既有线路长度，利用既有线路与设计线路长度之差精确计算出拨后线路伸缩量，较传统计算方法有诸多优点。如从始端进行拨道路作业，可计算某测点累计拨后伸缩量，从累计伸缩量数据中可推断出因拨道而引起线路内力变化情况，计算成果精度高，对指导编制线路拨道作业方案具有重要意义。本计算过程较复杂性，通过编写计算机程序，可极大提高工作效率，为铁路曲线养护高标准、精细化和标准化打下坚实的基础。

如果是绳正法或偏角法整正曲线，只要先将实测正矢或偏角数据转化为坐标值，再以坐标法进行整正计算，这样可直接运用本公式-7进行拨后线路伸缩量计算。

文章来源:

原文名称：既有线拨道量与线路伸缩量的关系

文章作者：廖显军

作者信息：中国铁路南宁局集团有限公司

参考文献：