CPⅢ测量控制网是高速铁路无砟轨道铺设施工和运营维护的定位基准[1],它是沿铁路线布设的三维控制网,分为CPⅢ(trackcontrolpointⅢ)平面控制网和高程控制网(简称CPⅢ平面网和CPⅢ高程网),一般在线下工程施工完成后布设和施测.CPⅢ控制网的主要特点[2]是:控制点数量多,沿线路方向每隔60m左右布设一对,点对的横向间距约为10~20m;精度要求很高,平面网要求相邻点的相对点位中误差不大于±1mm[3],高程网要求相邻点的高差中误差不大于±0.5mm,高程网测量应达到二等水准测量精度等级的要求[4];CPⅢ高程网虽与CPⅢ平面网共点,但采用不同的测量标志,分别进行平面网和高程网的测量;传统的CPⅢ高程网测量,都是采用电子水准仪按照特定的观测程序和路线进行测量,既有德国的中视法,又有中国的矩形法[5].
为克服高速铁路CPⅢ控制网将平面和高程数据分开测量的不足,提高高速铁路CPⅢ控制网的建网效率,并保证达到高精度要求,本文在CPⅢ平面控制网自由测站观测的基础上,提出采用同步观测的平面网数据进行CPⅢ三角高程网数据处理的新思路.理论分析和实践验证表明,CPⅢ三角高程网完全可以取代CPⅢ水准网[6],实现CPⅢ控制网一次测量即可获得平面网的坐标成果和高程网的高程成果,只用一种测量标志,就可实现建立CPⅢ三维网的目标[7].该技术是一项自主创新技术,已被高速铁路工程测量规范[6]采用.
文献[8-9]对CPⅢ三角高程网的建网原理及其可行性进行了定性和定量分析.本文介绍CPⅢ三角高程网的几何模型,重点是CPⅢ三角高程网平差计算原理,并建立了平差计算和精度评定的数学模型,最后,介绍根据该数学模型开发的实用CPⅢ三角高程网平差计算软件.
1 CPⅢ三角高程网几何模型
CPⅢ三角高程网是在CPⅢ平面网的基础上建立的.CPⅢ平面网是采用智能型全站仪自动观测的自由测站边角交会控制网,其观测值是自由测站到CPⅢ点的水平方向值、斜距和竖直角.采用自由测站观测,没有仪器对中的问题,棱镜中心就是CPⅢ三维控制点的点位,没有目标对中和棱镜高度问题.这样,根据自由测站到CPⅢ点的斜距和竖直角,就可以计算测站到CPⅢ点的三角高差.一个CPⅢ平面网测站一般观测12个CPⅢ点,由单个自由测站观测值形成的三角高差情况,如图1所示.S003为自由测站,CP301~CP312为该测站观测的12个CPⅢ点.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
CPⅢ平面网的每个CPⅢ点至少被3个测站观测[10],多个自由测站形成的三角高差见图2.
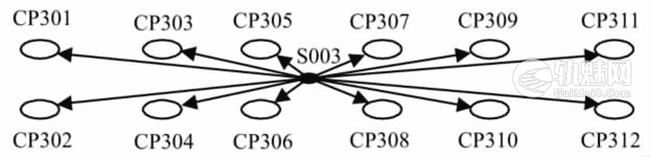
图1 单个测站观测值形成的三角高差
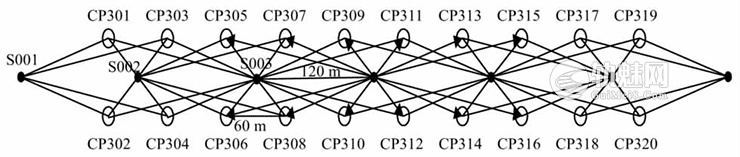
图2 多个自由测站观测值形成的三角高差
图2为根据多个自由测站到各CPⅢ点的单向三角高差构成的CPⅢ三角高程网.由于采用单向三角高差,地球曲率和大气折光的影响较显著,因此,采用未加改正的单向高差会影响高程成果的精度,无法满足CPⅢ高程网的要求.
用中间法计算三角高程可显著减弱甚至消除地球曲率和大气折光的影响,且不需考虑仪器高度.因此,可用中间法三角高程测量原理对图2的CPⅢ三角高程网进行改造.改造的思路是利用测站到CPⅢ点的直接高差,计算相邻CPⅢ点之间的间接高差,如图2所示,可用测站S003到CPⅢ中点CP301与CP302的直接高差,计算这两个相邻CPⅢ点之间的间接高差,其它相邻CPⅢ点之间的间接高差的计算原理类似.按上述思路,根据中间法三角高程原理,改造后的单个自由测站的CPⅢ三角高程网的网形如图3所示.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
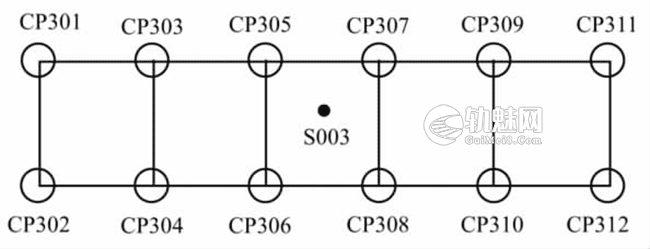
图3 改造后单个自由测站形成的CPⅢ三角高程网
改造后的多个自由测站CPⅢ三角高程网的网形如图4所示.严格地讲,改造后相邻点之间的间接高差已不再是独立观测值,而是相关观测值.
图4是基于自由测站观测值、精度达到二等水准测量精度等级和满足CPⅢ高程网精度要求的CPⅢ三角高程网的网形.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
从图4可见,由于每个CPⅢ点都有3个自由测站对其进行观测,因此,用自由测站点与CPⅢ点之间的直接高差计算得到的相邻两个CPⅢ点之间的间接高差,存在重复观测的情况,即每两个相邻CPⅢ点之间均有2个或3个高差观测值,在后续的数据平差计算时都应考虑这些情况.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
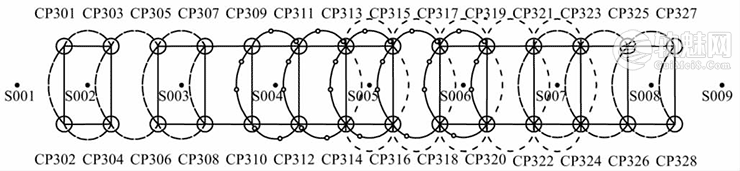
图4 改造后多个自由测站形成的CPⅢ三角高程网
2 CPⅢ三角高程网平差数学模型
间接平差根据控制网的观测值列出误差方程.误差方程规律性较强,容易编程求解.因此,CPⅢ三角高程网平差计算也可用间接平差[11].
2.1未知参数近似值的计算
计算CPⅢ三角高程网的间接平差,以CPⅢ点的高程作为未知参数.在求取常数项时,需要用到CPⅢ点的高程近似值.如果不给出CPⅢ点高程近似值,误差方程就无法列出.因此,列出间接高差误差方程之前,必须进行高程近似值的计算.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
CPⅢ三角高程网高程近似值的计算,主要采用与水准网测量平差近似高程推算相似的思路,即搜索三角高程网中与已知点发生联系的CPⅢ点,先计算出此CPⅢ点的近似高程,并将其作为新的已知点,再循环搜索,直到求出所有CPⅢ点的近似高程.在推算CPⅢ点近似高程时,需要用到相邻CPⅢ点之间的间接三角高差.按照中间法计算三角高程的原理,间接三角高差由自由测站到CPⅢ点的直接三角高差计算得出.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
2.2高差误差方程式
在推算出CPⅢ点近似高程后,即可建立间接三角高差观测值的误差方程.由中间法三角高程原理可知CPⅢ三角高程网的间接三角高差观测值.先用自由测站点到CPⅢ点之间的斜距和竖直角计算直接高差;再用同一测站到相邻两CPⅢ点之间的直接高差,计算两相邻CPⅢ点之间的间接高差.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
因此,CPⅢ三角高程网间接平差的误差方程与水准网间接平差的误差方程差异较大.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
以图4为例,介绍CPⅢ三角高程网高差误差方程式的建立过程.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
假定两相邻CPⅢ点\(i\)和\(j\)的高程平差值分别为\(\hat{X}_i\)和\(\hat{X}j\),近似高程分别为\(\hat{X}_{i0}\)和\(\hat{X}_{j0}\),高程改正数分别为\(\hat{X}_i\)和\(\hat{X}_j\).通过自由测站测出CPⅢ点\(i\)和\(j\)的直接高差,计算出\(i\)与\(j\)之间的间接三角高差为\(h_{ij}\),其改正数为\(v_{h_ij}\),则观测值误差方程为:󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$h_{ij}+v_{hij}=\hat{X}_j-\hat{X}_i \qquad (1)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
高程平差值等于近似高程加上其改正数,式( 1) 可改写为:󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$h_{ij}+v_{hij}=\hat{X}_j-\hat{X}_i+X_{io}-X_{jo} \qquad (2)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
整理式( 2) ,可得相邻CPⅢ点之间的间接三角高差误差方程:󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$v_{hij}=\hat{X}_j-\hat{X}_i-[h_{ij}-(X_{jo}-X_{io})] \qquad (3)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
式( 3) 中,hij的计算未考虑三角高程测量时球气差的影响. 若考虑球气差的影响,则间接三角高差误差方程为:󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$v_{hij}=\hat{X}_j-\hat{X}_i-[h_{ij}+(C_{j}-C_{i})-(X_{jo}-X_{io})] \qquad (4)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$C_i=\frac{1-K}{2R}(S_i \cos a_i)^2\\C_j=\frac{1-K}{2R}(S_j \cos a_i)^2$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
式中: K———大气折光系数;
R———地球曲率半径;
2.3 高差观测值权的确定
[login]
要对CPⅢ三角高程网中的间接高差观测值进行间接平差,需要建立网中相邻CPⅢ点之间高差观测值的权比关系. 水准网间接平差,往往按照经验定权法确定网中高差观测值的权重,即以1 km高差观测值为单位权观测值,各测段高差的权与该测段水准路线长度的公里数成反比. 而CPⅢ三角高程网不同于水准网,其直接观测值包括斜距和竖直角两类观测值,因此,CPⅢ三角高程网的合理定权问题,是亟待解决的关键问题之一.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
文献[12]认为三角高程各测段高差的权与测段长度公里数的平方成反比,但这不适合CPⅢ三角高程网,因为CPⅢ三角高程网中的高差不是传统意义上的三角高程测量的直接高差,而是通过两段三角高程测量的直接高差进一步求差后得到的.因此,应进一步研究CPⅢ三角高程网中高差的定权问题.
在CPⅢ三角高程网中,高差的测量误差与自由测站到两CPⅢ点的斜距和竖直角测量误差有关. 根据斜距与竖直角的测量中误差,按照误差传播规律求出CPⅢ三角高程网中高差的中误差,进而确定CPⅢ三角高程网中各高差的权值.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
上述CPⅢ点之间的间接高差是用自由测站与两CPⅢ点之间的直接高差计算得到的,因此,两相邻CPⅢ点之间\(i\)和\(j\)之的高差为:󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$h_{ij}=S_j\sin\alpha_j-S_i\sin\alpha_i\qquad(5)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
对式( 5) 全微分,可得:
$$dh_{ij}=\sin\alpha_idS_j+S_j\cos\alpha_j\frac{d\alpha_j}{{\rho}”}-\sin\alpha_idS_j-S_i\cos\alpha_i\frac{d\alpha_j}{{\rho}”}\qquad (6)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
式中:\(\rho”=206256”\) .󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
对式( 6) 运用误差传播律,可得高差中误差与竖直角和斜距测量中误差的关系为[13]:
$$m^2_{hij}=\sin^2\alpha_jm^2_{sj}+(S_j\cos\alpha_j)^2(\frac{m_{aj}}{{\rho}”})^2+\sin^2\alpha_jm^2_{sj}+(S_i\cos\alpha_i)^2(\frac{m_{ai}}{{\rho}”})^2\qquad (7)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
式中: \(m_{hij}\)———两相邻CPⅢ点\(i\) 和\(j\)高差的中误差;󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
\(m_{si}、m_{sj}\)———测站到\(i\) 和\(j\)两点斜距测量的中误差;󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
\(m_{ai}、m_{aj}\)———测站到两点\(i\) 和\(j\)竖直角测量的中误差.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
\(m_{si}、m_{sj}\)和\(m_{ai}、m_{aj}\)可根据全站仪的标称精度确定.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
以全站仪竖直角测量的标称精度\(\delta_0\)作为单位权中误差,则CPⅢ点\(i\) 和\(j\)之间高差观测值的权为:󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$w_{hij}=\frac{\delta_0^2}{m^2_{hij}}\qquad(8)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
用CPⅢ平面网观测时,每个CPⅢ点均有3 个自由测站对其进行角度和斜距观测,因此,根据自由测站与两CPⅢ点之间的高差,计算两个CPⅢ点之间的高差时存在同名高差[10],即每两个CPⅢ点之间均有多个高差观测值. 在合并同名高差时,由不同测站观测值计算得到的同名高差精度不同,应该采用加权平均方法进行合并. 设\(h_1\)和\(h_2\)为由不同自由测站观测值计算得到的同名高差,权分别为\(w_1\)和\(w_2\). 合并后的高差\(h\)的权为\(w_s\) . 同名高差加权合并后的高差为:
$$h=\frac{w_1h_1+w_2h_2}{w_1+w_2}\qquad (9)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
因为两个自由测站计算得到的同名高差相互独立,对式( 9) 运用权倒数传播得到:󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$\frac{1}{w_s}=(\frac{w_1}{w_1+w_2})^2\frac{1}{w_1}+(\frac{w_2}{w_1+w_2})^2\frac{1}{w_2}=\frac{1}{w_1+w_2}\qquad(10)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
2.4 法方程组成及其求解
根据式( 4) ,可构建CPⅢ三角高程网观测值误差方程的系数矩阵B 和常数项l; 权矩阵W 可通过式( 10) 确定,在确定权矩阵W 时忽略了相邻点之间高差的相关性. 建立法方程后,高程改正数为:󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$\hat{X}=(B^TWB)^{-1}B^TWL\qquad (11)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
高程改正数\(\hat{x}\)加上高程近似值\(X_0\)得到高程平差值\(\hat{X}\). 高差平差值\(\hat{h}\)可由高差观测值\(h\)加上其改正数\(v\)得到,高差改正数为:󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$v=B\hat{x}-l\qquad (12)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
2. 5 精度评定
CPⅢ三角高程网间接平差完成后,利用观测值权矩阵、平差后得到的改正数、高程协因数阵等信息,可以进行CPⅢ三角高程网平差精度的评定,主要是评定网中各CPⅢ点高程的精度和相邻CPⅢ点之间高差的相对精度.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(1) 评定网中各CPⅢ点高程的精度.平差后观测值单位权中误差为:󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$\sigma _0=\pm \sqrt{\frac{V^TWV}{r}}=\pm \sqrt{\frac{V^TWV}{n-t}}\qquad (13)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
式中: \(V^TWV\)———观测值改正数的加权平方和;󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
\(n\)———观测值个数;
\(t\)———必要观测值个数;󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
\(r\)———多余观测值个数.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
CPⅢ三角高程网平差以CPⅢ点的高程作为未知参数,根据间接平差原理可得未知参数协因数矩阵为:󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$\hat{Q}_{\hat{X}}=(B^TWB)^{-1}$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
\(\hat{Q}_{\hat{X}}\)中的对角线元素\(\hat{Q}_{\hat{X}_K\hat{X}_K}\)称为第\(k\)个未知数的权倒数[14]. 平差后CPⅢ三角高程网的方差矩阵为:
$$\hat{D}_{\hat{X}_K\hat{X}_K}=\delta^2_0
\begin{bmatrix}
Q_{\hat{X}_1\hat{X}_1}Q_{\hat{X}_1\hat{X}_2} \cdots Q_{\hat{X}_1\hat{X}_n} \\
Q_{\hat{X}_2\hat{X}_1}Q_{\hat{X}_2\hat{X}_2} \cdots Q_{\hat{X}_2\hat{X}_n} \\
\vdots\vdots \vdots \vdots \\
Q_{\hat{X}_n\hat{X}_1}Q_{\hat{X}_n\hat{X}_2} \cdots Q_{\hat{X}_n\hat{X}_n} \\
\end{bmatrix}=
\begin{bmatrix}
D_{\hat{X}_1\hat{X}_1}D_{\hat{X}_1\hat{X}_2} \cdots D_{\hat{X}_1\hat{X}_n} \\
D_{\hat{X}_2\hat{X}_1}D_{\hat{X}_2\hat{X}_2} \cdots D_{\hat{X}_2\hat{X}_n} \\
\vdots\vdots \vdots \vdots \\
D_{\hat{X}_n\hat{X}_1}D_{\hat{X}_n\hat{X}_2} \cdots D_{\hat{X}_n\hat{X}_n} \\
\end{bmatrix}\qquad (14)$$
待定点平差后的高程中误差可按下式计算:󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$m_{\hat{X}_K\hat{X}_K}=\sigma_0\sqrt{Q_{\hat{X}_K\hat{X}_K}}\qquad(15)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(2)推导相邻CPⅢ点之间高差中误差的精度评定公式.根据平差后相邻两CPⅢ点\(i\)和\(j\)的高程平差值\(\hat{X}_i\)和\(\hat{X}_j\),点\(i\)和\(j\)之间的高差平差值为:󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$\hat{h}_{ij}=\hat{X}_j-\hat{X}_i\qquad(16)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
对式(16)运用协因数传播律,可得相邻两CPⅢ点\(i\)和\(j\)之间高差的协因数为:󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$\hat{h}_{ij}=\hat{x}_j-\hat{X}_j\qquad(17)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
由间接平差随机模型可知,任意相邻两CPⅢ点\(i\)和\(j\)之间高差的中误差为:󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$m_{\hat{h}_{ij}}=\sigma_0\sqrt{Q_{\hat{h}_{ij}}}\qquad(18)$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
式(16)~(18)是相邻CPⅢ点之间高差相对中误差的计算过程,CPⅢ高程网要求相邻点的高差中误差\(m_{\hat{h}_{ij}}\)不大于±0.5mm.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
3 CPⅢ三角高程网平差计算软件及计算验证
3.1平差计算软件
根据上面推导的CPⅢ三角高程网平差的数学模型以及精度评定公式(13)~(18),运用VisualC#语言研制了CPⅢ三角高程网平差计算软件.该软件主要功能及其计算流程为:󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
①平差参数设置,主要是设置仪器的标称精度和确定是否加入球气差改正.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
②生成平差文件,利用CPⅢ平面网自由测站观测值生成带权的间接高差文件,为后续平差计算做准备.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
③高差较差检查,检查同名高差或往返测高差的较差是否满足要求.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
④导入已知数据,为平差提供一个高程基准.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
⑤闭合差搜索,搜索出CPⅢ三角高程网的附合或闭合路线闭合差.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
⑥网平差处理,用生成的平差文件和已知高程数据进行平差处理,并进行精度评定.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
3.2计算验证
为证明按本文方法建立的CPⅢ三角高程网精度能够达到二等水准的精度,在某高速铁路的CPⅢ平面网中,随机抽取了12个区段约50km的自由测站观测值,在满足闭合环和附合路线闭合差小于二等水准的限差要求后,用本文方法和软件计算了这12个区段CPⅢ三角高程网的每公里高差全中误差和偶然中误差,结果见表1.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
表1 CPⅢ三角高程网每公里高差全中误差和偶然中误差计算结果
| 误差 | 区段序号 | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 全中误差 | 0.41 | 0.41 | 0.01 | 0.02 | 0.29 | 0.31 | 0.32 | 0.38 | 0.31 | 0.33 | 0.35 | 0.30 |
| 偶然中误差 | 0.45 | 0.52 | 0.77 | 0.93 | 0.51 | 0.37 | 0.37 | 0.51 | 0.77 | 0.55 | 0.48 | 0.49 |
从表1可见:12个区段CPⅢ三角高程网满足每公里高差全中误差不大于±2.0mm和每公里偶然中误差不大于±1.0mm[15]的二等水准限差要求,因此,CPⅢ三角高程网能达到二等水准的精度等级.
为进一步验证本文方法的可行性和精度,在某高速铁路随机抽取了约330km共10858个点的CPⅢ网,用本文的方法和软件计算了各点三角高程,并与水准测量的同名高程进行比较,见表2.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
表2 CPⅢ点三角高程与相应水准高程的比较
| 项目 | 高程较差区间/mm | ||||
| 0.0~1.0 | 1.0~2.0 | 2.0~3.0 | 3.0~4.0 | 4.0~5.0 | |
| CPⅢ点数 | 8 536 | 1 895 | 361 | 53 | 13 |
| 比例/% | 78.61 | 17.46 | 3.32 | 0.48 | 0.12 |
从表2可见:
高程较差落入[-1mm,1mm]区间的有8536个,占78.61%;󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
高程较差落入[-2mm,2mm]区间的有10431个,占96.07%;󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
高程较差落入[-3mm,3mm]区间的有10792个,占99.40%.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
这说明10858个CPⅢ三角高程与其水准高程的差值绝大部分不大于±3mm,仅0.60%大于±3mm.可见CPⅢ三角高程网高程与其水准高程相差较小,99.40%以上差值不大于±3mm,因此,CPⅢ三角高程网可以代替CPⅢ水准网;同时,也表明忽略相邻间接高差的相关性,对平差结果几乎没有影响.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
4 结论
(1)根据CPⅢ三角高程网的建网测量原理,推导了CPⅢ三角高程网间接平差及其完整精度评定的数学模型.理论分析表明,该数学模型能够满足CPⅢ高程网严密平差计算和精度评定的特殊要求.
(2)推导了相邻CPⅢ点之间的间接高差定权公式,对CPⅢ三角高程网中重复观测高差,采用加权平均合成方法.实例表明,该方法计算结果与水准测量结果吻合程度较高,说明该方法高效可行,能够满足CPⅢ高程网的高精度要求.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(3)根据本文推导的数学模型开发的CPⅢ三角高程网平差计算软件,能够自动读取CPⅢ平面网自由测站观测值,计算网中相邻CPⅢ点之间的间接高差,自动合成同名观测值并定权,探测网中所有闭合和附合路线的闭合差以及自动计算每公里高差的全中误差,最后进行全网的严密平差和精度评定.该软件已通过铁道部建设司的测试和评审.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(4)本文提出的CPⅢ高程网建网测量及数据处理新方法,可以不进行水准测量建立CPⅢ高程网,提高了CPⅢ控制网测量的效率,具有实用价值.󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
[/login]
文章来源:
原文名称:高速铁路CPⅢ三角高程网构网与平差计算方法󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
作者信息:刘成龙1, 杨雪峰1, 卢建康2, 何波1( 1. 西南交通大学地球科学与环境工程学院,四川成都610031; 2. 中铁二院工程集团有限责任公司,四川成都610031)
原文出处:西南交通大学学报第46卷󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
参考文献:[s][p]
- [1] 中华人民共和国铁道部. 铁建设[2006]189 号客运专线无碴轨道铁路工程测量暂行规定[S]. 北京: 中国铁道出版社, 2006.
- [2] 刘成龙,杨友涛,徐小左. 高速铁路CPⅢ交会网必要测量精度的仿真计算[J]. 西南交通大学学报, 2008,43( 6) : 718-723.
- [3] 王平,陈嵘,陈小平. 高速铁路道岔设计关键技术
- [4] 程昂,刘成龙,徐小左. CPⅢ平面网必要点位精度的研究[J]. 铁道工程学报, 2009( 1) : 44-48.
- [5] 李书亮,刘成龙,倪先桃. 高速铁路CPⅢ高程控制网测量方法研究[J]. 测绘科学, 2011, 36( 1) : 45-47.
- [6] 中华人民共和国铁道部. TB 10601—2009 高速铁路工程测量规范[S]. 北京: 中国铁道出版社, 2009.
- [7] 中华人民共和国铁道部. TB 10101—2009 铁路工程测量规范[S]. 北京: 中国铁道出版社, 2009.
- [8] 西南交通大学. CPⅢ高程网建网测量及其标准的研究报告[R]. 成都: 西南交通大学, 2009.
- [9] 付建斌,刘成龙,卢建康,等. 基于自由测站的高速铁路CPⅢ高程控制网建网方法研究[J]. 铁道工程学报, 2010( 12) : 33-36.
- [10] 王鹏,刘成龙,杨希. 无碴轨道CPⅢ自由设站边角交会网平差概略坐标计算方法研究J]. 铁道勘察, 2008( 3) : 26-28.
- [11] 张忠良,杨友涛,刘成龙. 轨道精调中后方交会点三维严密平差方法研究[J]. 铁道工程学报,2008( 5) : 33-36.
- [12] 武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉: 武汉大学出版社,2003:
- 118-119.
- [13] 杨雪峰,龚涛,汪精河. 测量平差中求解协因数的简化算法[J]. 测绘科学, 2009, 34( 1) : 85-86.
- [14] 倪先桃. 无砟轨道CPⅢ高程控制网测量与数据处理方法研究[D]. 成都: 西南交通大学, 2009.
- [15] 中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会. GB/T 12897—2006 国家一、二等水准测量规范[S]. 北京: 中国标准出版社, 2006.
[/p]




感谢感谢