既有铁路曲线在经过长期运营后，其平面线型会发生变化，曲线的偏角、半径、缓和曲线长度等线型参数与最初的设计值不符，需要对这些发生变化后的参数进行整正，将已变形的曲线恢复到标准线型。
因坐标法理论严密而优于绳正法和偏角法 [1]，目前主要应用在增建二线、改建既有铁路曲线及线路大中修，传统的坐标法整正，将始终端切线作固定直线作为常量，只优化缓和曲线与半径，因优化变量有限，曲线整正通常会遗漏最佳方案。
1 坐标法整正的基本原理
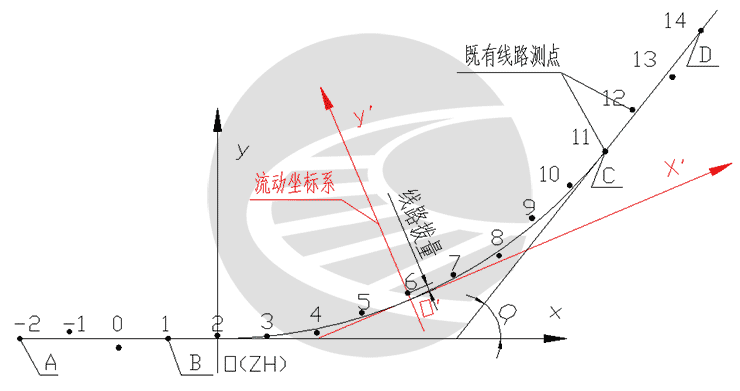
如图1，以，在优化出缓和曲线长和半径值后， 沿线路中心线始点A至终D点范围内以某点的坐标为原点，以切线方向为横坐标轴，建立流动坐标系X’-O’-Y’。各既有测点在流动坐标系中横坐标值，则认为测点落在坐标纵轴上，则对应的Y值即为拨量，拨量方向：左转曲线，正值向外挑，反之向下压，整正计算有多种计算方法，可参考相关书籍了解[2]，此处从略。
图1 坐标法整正曲线示意图
2 传统坐标法整正的变量参数存在的问题
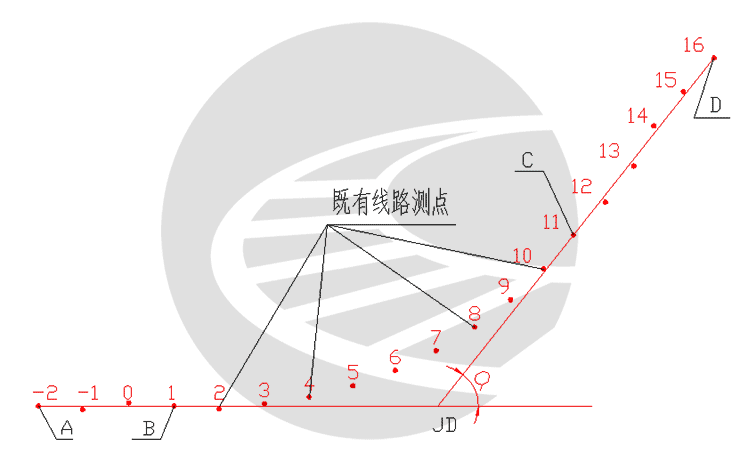
传统的坐标法整正计算，如图2，通常是先在始、终端既有直线上任意分别取两点A、B和C、D求出两端直线方程，然后联立解方程求出交点坐标JD，将两端切线作为常量，优化两端缓和曲线l0和半径R，共有3个变量，许多文献均按此方法整正计算。实际上，两端切线相对于的既有线平面位置，对曲线整正影响是相当大的，因为它可以影响曲线转角大小，同时影响到在一定的缓和曲线与半径条件下曲线的平面形状，当然也影响到设计曲线轨迹与既有线各测点的相对位置，拨量受影响较大。特别是出现大拨量的情况下，现场无法作业，如果在电气化铁路地段，线路抬道、拨道数量均有严格规定，传统的两端缓和曲线l0和半径R共3个变量无法满足要求，需要另外增加始、终切旋转2个变量，合计5个变量的曲线整正新方法，才能解决问题。
图2 传统坐标法整正曲线切线位置图
3 以两端切线为变更参与曲线整正优化
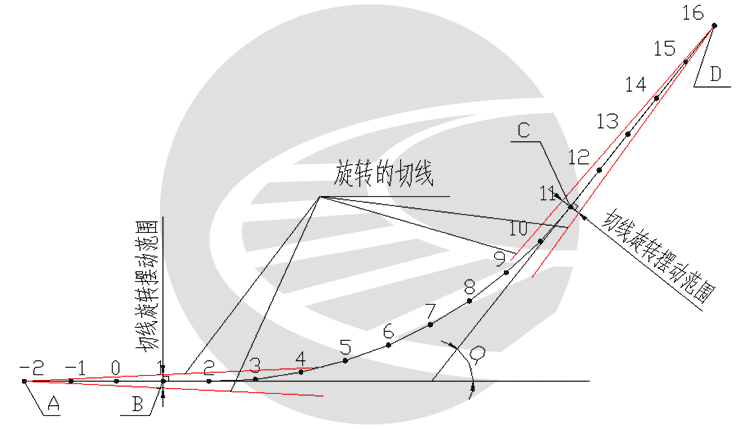
在初步选定的始终端切线桩A、B的基础上，以最始、终端的A、D为固定点，B、C点作为动点在切线的法方向移动，确定移动范围，按步长0.1mm从左至右移动进行扭转，分别按每扭转一步长，配一组切线进行优化，以缓和曲线长l0和半径R为变量或半径R为变量进行优化，求出一组目标函数，最后对所有目标函数进行筛选，找出最佳目标函数值（通常用拨量绝对值之和或最大拨绝对值最小）寻找最优解，如图3所示。
图3 切线扭转优化曲线要素图
4 算例
以某发表的坐标法整正曲线文献[3]为例，根据表1所示，文献中曲线整正第1、16、37和50号桩的拨量均为0mm，相当于以第1、16、37和50号桩为固定确定切线方向，曲线转角α=4°55′48″。而新方法在原文献固定确定切线方向的基础上，以第1、50号桩固定不变，经过优化将第16号桩向切线法线方向移动0.2mm（拨量-0.2 mm），37号桩移动30.1mm（拨量-30.1mm），曲线转角为α=4°55′24.62″，以最大拨绝对值最小作为目标函数优化曲线要素，曲线整正优化成果如表1。
表1 两端切线参与整正方法计算表
| 编号 | 始缓长L1 | 终缓长L2 | 半径R | 曲全长LY | 始切长T1 | 终切长T2 | 曲线偏角a | 曲线转向 | ||
| 39 | 50 | 50 | 3128.02 | 318.795 | 159.482 | 159.482 | 4°55′24.6″ | 左转 | ||
| 测点 | 实测X坐标(m) | 实测Y坐标(m) | 既有线里程 | 控制拨量(mm) | 拨道量(mm) | 线形 | 超高(mm) | 设计里程(m) | 拨后伸缩量(mm) | 文献拨量mm |
| 1 | 198.575 | -12.494 | 定点1 | 0 | 直 | 0 | -214.47 | 0 | 0 | |
| 2 | 178.472 | -12.112 | 228020 | -5 | 直 | 0 | -194.36 | 0 | -5 | |
| 3 | 168.735 | -11.933 | 228030 | -1.4 | 直 | 0 | -184.62 | 0 | -2 | |
| 4 | 158.511 | -11.739 | 228040 | -3.7 | 直 | 0 | -174.4 | 0 | -3 | |
| 5 | 138.498 | -11.367 | 228060 | -0.3 | 直 | 0 | -154.38 | 0 | 0 | |
| 6 | 128.5 | -11.175 | 228070 | -4.8 | 直 | 0 | -144.38 | 0 | -5 | |
| 7 | 115.151 | -10.921 | 228083 | -8.5 | 直 | 0 | -131.03 | 0 | -8 | |
| 8 | 108.497 | -10.802 | 228090 | -2.7 | 直 | 0 | -124.37 | 0 | -3 | |
| 9 | 98.49 | -10.614 | 228100 | -3.1 | 直 | 0 | -114.36 | -0.1 | -3 | |
| 10 | 87.777 | -10.415 | 228111 | -1.2 | 直 | 0 | -103.65 | 0 | -1 | |
| 11 | 78.486 | -10.24 | 228120 | -1.9 | 直 | 0 | -94.356 | -0.1 | -2 | |
| 12 | 67.82 | -10.039 | 228131 | -2.9 | 直 | 0 | -83.689 | 0 | -3 | |
| 13 | 58.479 | -9.867 | 228140 | 0.3 | 直 | 0 | -74.346 | 0 | 0 | |
| 14 | 48.469 | -9.678 | 228150 | -1 | 直 | 0 | -64.334 | 0 | -1 | |
| 15 | 38.474 | -9.49 | 228160 | -1.5 | 直 | 0 | -54.337 | 0 | -2 | |
| 16 | 28.484 | -9.304 | 定点2 | -0.2 | 直 | 0 | -44.346 | 0 | 0 | |
| 17 | 17.774 | -9.099 | 228181 | -4.3 | 直 | 0 | -33.634 | 0 | -5 | |
| 18 | -6.648 | -8.638 | 228205 | -7.4 | 直 | 0 | -9.2073 | 0 | -8 | |
| 19 | -21.55 | -8.366 | 228220 | -0.1 | 缓 | 0 | 5.6972 | 0 | 0 | |
| 20 | -41.552 | -8.015 | 228240 | 6.1 | 缓 | 0 | 25.7023 | 0 | 5 | |
| 21 | -61.547 | -7.722 | 228260 | 4.5 | 缓 | 0 | 45.6995 | 0 | 1 | |
| 22 | -81.558 | -7.533 | 228280 | -5.8 | 圆 | 0 | 65.7114 | 0 | -11 | |
| 23 | -101.566 | -7.474 | 228300 | -14 | 圆 | 0 | 85.7194 | -0.1 | -20 | |
| 24 | -121.572 | -7.542 | 228320 | -23.2 | 圆 | 0 | 105.726 | -0.2 | -30 | |
| 25 | -141.572 | -7.738 | 228340 | -32.3 | 圆 | 0 | 125.726 | -0.4 | -39 | |
| 26 | -161.574 | -8.069 | 228360 | -34.3 | 圆 | 0 | 145.731 | -0.6 | -39 | |
| 27 | -181.575 | -8.536 | 228380 | -28.3 | 圆 | 0 | 165.737 | -0.8 | -30 | |
| 28 | -201.564 | -9.134 | 228400 | -18.9 | 圆 | 0 | 185.735 | -0.9 | -18 | |
| 29 | -221.55 | -9.864 | 228420 | -5.3 | 圆 | 0 | 205.734 | -1 | 0 | |
| 30 | -241.534 | -10.729 | 228440 | 15.3 | 圆 | 0 | 225.737 | -1 | 26 | |
| 31 | -261.521 | -11.711 | 228460 | 24.8 | 圆 | 0 | 245.748 | -0.8 | 42 | |
| 32 | -281.498 | -12.819 | 228480 | 32.6 | 圆 | 0 | 265.756 | -0.7 | 57 | |
| 33 | -301.468 | -14.038 | 228500 | 28.8 | 缓 | 0 | 285.764 | -0.5 | 59 | |
| 34 | -321.42 | -15.322 | 228520 | 6.6 | 缓 | 0 | 305.757 | -0.4 | 40 | |
| 35 | -331.714 | -15.999 | 228531 | -6.7 | 缓 | 0 | 316.073 | -0.5 | 27 | |
| 36 | -341.383 | -16.634 | 228540 | -22.1 | 直 | 0 | 325.763 | -0.5 | 11 | |
| 37 | -361.343 | -17.969 | 定点3 | -30.1 | 直 | 0 | 345.768 | -0.5 | 0 | |
| 38 | -381.317 | -19.308 | 228580 | -34.9 | 直 | 0 | 365.786 | -0.5 | -7 | |
| 39 | -401.28 | -20.654 | 228600 | -32.1 | 直 | 0 | 385.795 | -0.5 | -6 | |
| 40 | -421.233 | -22 | 228620 | -28.5 | 直 | 0 | 405.793 | -0.5 | -5 | |
| 41 | -441.192 | -23.346 | 228640 | -25.4 | 直 | 0 | 425.797 | -0.4 | -5 | |
| 42 | -461.156 | -24.689 | 228660 | -25.6 | 直 | 0 | 445.807 | -0.5 | -7 | |
| 43 | -481.113 | -26.035 | 228680 | -22.4 | 直 | 0 | 465.809 | -0.5 | -6 | |
| 44 | -501.073 | -27.382 | 228700 | -18.3 | 直 | 0 | 485.814 | -0.5 | -5 | |
| 45 | -523.877 | -28.923 | 228723 | -11.6 | 直 | 0 | 508.67 | -0.5 | 0 | |
| 46 | -540.994 | -30.077 | 228740 | -9.3 | 直 | 0 | 525.826 | -0.5 | 0 | |
| 47 | -560.953 | -31.427 | 228760 | -2.1 | 直 | 0 | 545.831 | -0.5 | 4 | |
| 48 | -580.913 | -32.769 | 228780 | -3.1 | 直 | 0 | 565.836 | -0.5 | 2 | |
| 49 | -600.877 | -34.116 | 228800 | 0.7 | 直 | 0 | 585.845 | -0.5 | 3 | |
| 50 | -620.848 | -35.459 | 定点4 | 0 | 直 | 0 | 605.861 | -0.5 | 0 | |
表2 两种整正方法计算结果比较表
| 整正方法 | 曲线转角 | 缓和曲线l01 m | 缓和曲线l02 m | 曲线半径R m | 拨量绝对值之和mm | 最大拨量值mm | 最小拨量值mm |
| 传统坐标法 | 4°55′48″ | 50 | 50 | 3151.01 | 556 | 59 | -39 |
| 新坐标法 | 4°55′24.62″ | 50 | 50 | 3128.02 | 603.9 | 32.6 | -34.9 |
如表2，在缓和曲线相同情况下，通过扭转两端切线方向，根据目标函数进行优化曲线半径，通过对比，新方法计算结果的最大拨量值和最小拨量值比传统的都要小，说明新方法整正的质量优于传统的方法。
三、结语
通过比较传统固定切线坐标法和增加切线作为变量参数坐标法整正曲线，说明扭转切线整正曲线质量明显优于传统方法。根据不同的目标函数，优化出相应的曲线要素和成果，在曲线整正道路上迈出重要的一步，特别是在电气化铁路、铁路桥梁和重要建筑物等对控制拨量有诸多限制要求曲线整正，提供了理论依据，为指导现场拨道作业具有重要意义。
文章出处:
原文名称:坐标法整正曲线变量参数的探讨
文章作者：廖显军
作者信息：中国铁路南宁局集团有限公司
文参考文献：[s][p]
- [1]何恩祥. 渐伸线整正既有曲线误差及适用范围[J]. 铁道工程学报, 1992（2）:94-97
- [2]中国铁路总公司运输局工务部 铁路工务技术手册（线路养护·大修）[S]. 北京 中国铁道出版社.2018 :39-54
- [3]张 伟 铁路既有线曲线整正方法的探讨 铁道建筑 [J] 2009年第11期 79-81
[/p]
