整正曲线方向的方法有多种,如以弦绳测量的绳正法、以仪器测量的偏角法、矢距法等,还有由激光和传感为导向,只要输入曲线要素,经电子计算机控制自动进行曲线拨正的大型养路机械拨道法。绳正法又分流水拨道法和简易拨道法两种,其基本原理一样,只是计算方法有所不同。流水拨道法中又有修正差累计、修正计划正矢和修正半拨量等几种方法。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
偏角法和矢距法多用于工程部门,大型养路机械拨道用于周期性维修和重点病害整治,工务部门维修养护最常用的方法是绳正法。本文着重介绍绳正法整正曲线的基本原理和计算方法。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
1. 两个假定
(1)假定曲线两端切线方向不变(即曲线始终点拨量为零)。切线方向不变,也就是曲线转角不变,即Σƒi=Σƒj(即现场正矢合计=计划正矢合计)。同时曲线两端直线不发生平行移动(即曲线始终点拨量为零),即
$$\Delta E_{sh}=\Delta E_{zh}=2\sum_{0}^{i-1}\sum_{0}^{i-1}df=0$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
式中
ΔEsh———曲线始点拨量;
ΔEzh———曲线终点拨量;
\(2\sum_{0}^{i-1}\sum_{0}^{i-1}df\)全拨量,即为两倍的正矢差累计的合计。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(2)假定曲线上任一点拨动,对相邻点在长度上并不随之移动,拔动后钢轨总长不变,如图1所示。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
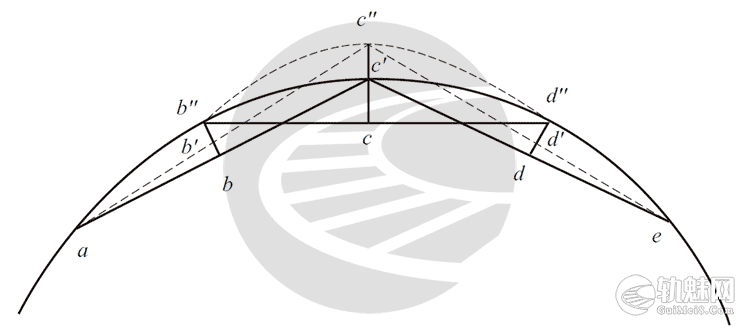
图1 线形变化示意
当c′点向外拨动至c″时,b″、d″两点受影响会产生位移,只是因为弦长为20m,b″、d″两点的移动量很小,可忽略不计,故假定其位置不变。
2. 四条基本原理
(1)等长弦分圆曲线为若干弧段,则每弧段正矢相等(即曲线上各点正矢之和为一常数)。如图1所示,弦ac″=c″e,其相对应的正矢b′b″=d′d″。
(2)曲线上任一点拨动,对相邻点均有影响,其影响量为拨动点拨动量的二分之一,方向相反,如图2所示。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
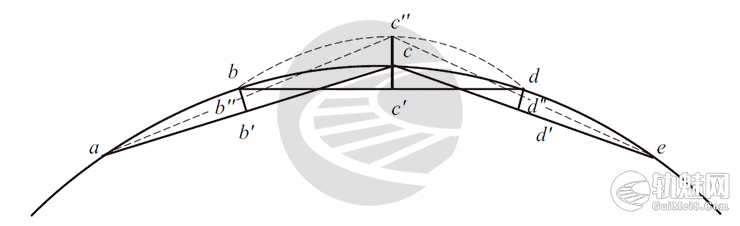
图2 拨量关系示意
从图2中可以看出,a、b、c、d、e 为圆弧上的等分点,当c 点向外拨动cc″时,其相邻点b、d 的正矢要减少\(\frac{cc”}{2}\)。
(3)拨道前与拨道后,整个曲线正矢总和不变(即现场正矢合计与计划正矢合计必须相等)。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(4)在拨道时,整个曲线各测点正矢发生的增减量总和必须为零(即曲线上各点正矢差的代数和为零)。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
3. 基本要求
(1)曲线两端直线轨向不良,一般应事先拨正,两曲线间直线较短时,可与两曲线同时计算、拨正;
(2)在外股钢轨上用钢尺丈量,每10m 设置一个测点;󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(3)在风力较小条件下,拉绳测量每个测点正矢,测量三次取平均值;󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(4)按绳正法计算拨道量,计算时不宜为减少拨道量而大量调整计划正矢;󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(5)设置拨道桩,按桩拨道。
4.曲线整正计算
(1)曲线中央点位置QZ:
$$QZ=\frac{现场正矢倒累计合计}{现场正矢合计}=\frac{\sum (f_i+f_{i-1}))}{\sum f_i}$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
由此式计算出的曲中点位置,是以测点号来表示其从测量正矢起点至曲中点的距离。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(2)圆曲线平均正矢fp:
①已知曲线半径,用下式求得fp(20m 或10m 弦):
$$f_p=\frac{50000}{R}或f_p=\frac{12500}{R}$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
② 不知曲线半径,用下式求得fp:
$$QZ=\frac{现场正矢合计}{测量正矢的测点数}=\frac{\sum f_i}{n}$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
式中 n———相对应测量正矢的测点数。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
注:现场采值一般取曲线中部数值大致相同的现场正矢。
(3)圆曲线分段数M :
$$M=\frac{现场正矢合计}{圆曲线平均正矢}=\frac{\sum f_i}{f_p}$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(4)圆曲线长度Ly:
Ly=M ×10m
(5)圆曲线头尾位置(ZY,YZ):
$$ZY=QZ-\frac{M}{2}\\YZ=QZ+\frac{M}{2}$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(6)缓和曲线的分段数m:
$$m=\frac{缓和曲线长度}{10}=\frac{L_h}{10}$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
如不知缓和曲线长度,可根据公式Lh=9Hνmax,或困难条件下Lh=7Hνmax,先求缓和曲线长度。
式中
Lh———缓和曲线长度(m);
H ———曲线超高值(mm);
νmax———线路容许速度(km/h)。
计算结果取10m 的整倍数。
(7)缓和曲线绐终点位置(ZH,HY,YH,HZ):
在圆曲线上加设缓和曲线,是将缓和曲线长度的一半放在圆曲线上,另一半放在直线上。也就是说,圆曲线的直圆点(ZY)和圆直点(YZ)分别是两个缓和曲线的中央点。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$ZH=直圆点-\frac{缓和曲线分段数}{2}=ZY-\frac{m}{2}\\HY=直圆点+\frac{缓和曲线分段数}{2}=ZY+\frac{m}{2}\\HY=圆直点-\frac{缓和曲线分段数}{2}=YZ-\frac{m}{2}\\HZ=圆直点+\frac{缓和曲线分段数}{2}=YZ+\frac{m}{2}$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(8)无缓和曲线时,整桩上,圆曲线始、终点正矢:
$$f_{HY(YH)}=\frac{圆曲线平均正矢}{2}=\frac{f_p}{2}$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(9)无缓和曲线时,圆曲线始、终点不在测点上的正矢:
从图3中可以看出第1、2测点和第5、6测点分别与直圆、圆直点相邻,其正矢f1 和f6、f2 和f5 可按下式计算:
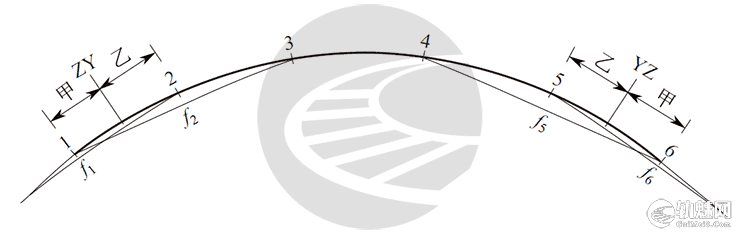
图3 圆曲线始终点不在测点上示意
$$f_1(或f_6)=\frac{乙^2}{2}\times f_p\\f_2(或f_5)=(1-\frac{甲^2}{2})\times f_p$$
式中
甲———圆曲线始(终)点至直线上相邻测点的距离;󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
乙———圆曲线始(终)点至圆曲线上相邻测点的距离。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(10)有缓和曲线,其始、终点(ZH、HY、YH、HZ)在测点上的正矢计算:
①始点正矢
$$f_{ZH}(或f_{HZ})=\frac{1}{6}\times f_d$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
②终点正矢
$$f_{HY}(或f_{YH})=f_p-\frac{1}{6}\times f_d$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
式中 fd———缓和曲线相邻各点的正矢递变率(‰)。
③缓和曲线上任意点的正矢fi
$$f_i=i_i\times f_d$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
或
$$f_i=x_i\times f_d$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(11)有缓和曲线,但始、终点不在测点上的正矢:
从图4中看出,测点2、3与直缓点(ZH)相邻,测点5、6与缓圆点(HY)相邻󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
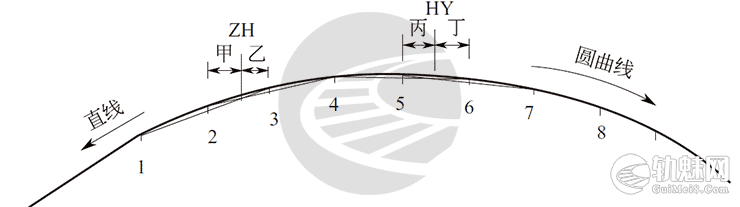
图4 缓和曲线始终点不在测点上示意
其正矢为
$$f_2=\frac{乙^3}{6}\times f_d\\f_3=\left ( \frac{甲^3}{6}+乙 \right )\times f_d\\f_5=f_p-\left ( \frac{丁^3}{6}+丙 \right )\times f_d\\f_6=f_p-\frac{丙^3}{6}\times f_d\\$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
5 例题
[login]
已知某曲线半径为800m,曲线长279.79m,缓和曲线长70m,实测正矢30点,现场正矢合计1321mm,现场正矢倒累计合计为19811mm,试计算各主要桩点位置、圆曲线长度及缓和曲线各点计划正矢,并图示。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
解:(1)曲中点QZ:
$$QZ=\frac{现场正矢倒累计合计}{现场正矢合计}=\frac{\sum (19811}{1321}=14.997$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
计算结果表示曲中点在测点14至15之间,距测点14为9.97m,距测点15为0.03m。如起点编号为“0”,在计算正矢时,桩号作为纵距应减去1。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(2)圆曲线平均正矢:
$$f_p=\frac{50000}{R}=\frac{50000}{800}=62.5mm,取63mm$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(3)圆曲线分段数M :
$$M=\frac{现场正矢合计}{圆曲线平均正矢}=\frac{1321}{63}=20.968$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(4)圆曲线长度:
$$L_y=M\times 10m=20.968\times 10m=209.68m$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(5)圆曲线头尾位置:
$$ZY=QZ-\frac{M}{2}=14.997-\frac{20.968}{2}=4.513\\YZ=QZ+\frac{M}{2}=14.997+\frac{20.968}{2}=25.481$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(6)缓和曲线分段数m:
$$m=\frac{L_h}{10}=\frac{70}{10}=7$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(7)缓和曲线始终点位置(即ZH、HY、YH、HZ):󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
$$ZH=ZY-\frac{m}{2}=4.513-\frac{7}{2}=1.013\\HY=ZY+\frac{m}{2}=4.513+\frac{7}{2}=8.013\\YH=YZ-\frac{m}{2}=25.481+\frac{7}{2}=21.981\\HZ=YZ+\frac{m}{2}=25.481+\frac{7}{2}=28.981$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(8)正矢递变率:
$$f_d=\frac{f_p}{m}=\frac{63}{7}=9 ‰$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
(9)不在整桩上的正矢计算:
$$f_1=\frac{乙^3}{6}\times f-d=\frac{0.987^3}{6}\times 9\approx 1.44mm,取1mm\\f_2=\left ( \frac{甲^3}{6}+乙 \right )\times f-d\left ( \frac{0.013^3}{6}+0.987 \right )\times 9\approx 8.88mm,取9mm\\f_3=x_3\times f_d=1.987\times 9=17.883mm,取18mm\\f_4=x_4\times f_d=2.987\times 9=26.883mm,取27mm\\f_5=x_5\times f_d=3.987\times 9=35.883mm,取36mm\\f_6=x_6\times f_d=4.987\times 9=44.883mm,取45mm\\f_7=x_7\times f_d=5.987\times 9=53.883mm,取54mm\\f_8=f_p-\left ( \frac{丁^3}{6}+丙 \right )\times f_d=63-\left ( \frac{0.987^3}{6}+0.013 \right )\times 9=61.44mm,取61mm\\f_9=f_p-\frac{丙^3}{6}\times f_d=63-\frac{0.013^3}{6}\times 9=63mm\\f_10\rightarrow f-{20}=f_p=63mm\\f_{29}\frac{乙^3}{6}\times f_d=\frac{0.981^3}{6}\times 9=1.42mm,取1mm\\f_{28}=\left ( \frac{甲^3}{6}+乙 \right )\times f_d=\left ( \frac{0.019^3}{6}+0.981 \right )\times 9=8.82mm,取9mm\\f_{27}=x_{27}\times f_d=1.981\times 9=17.829mm,取18mm\\f_{26}=x_{26}\times f_d=2.981\times 9=26.829mm,取27mm\\f_{25}=x_{25}\times f_d=3.981\times 9=35.829mm,取36mm\\f_{24}=x_{24}\times f_d=4.981\times 9=44.829mm,取45mm\\f_{23}=x_{23}\times f_d=5.981\times 9=53.829mm,取54mm\\f_{22}=f_p-\left ( \frac{丁^3}{6}+丙 \right )\times f_d=63-(\frac{0.981^3}{6}+0.019)\times 9=61.41mm,取61mm\\f_{21}=f_p-\frac{丙^3}{6}\times f_d=63-\frac{0.019^3}{6}\times 9=63mm$$󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
例题中的曲中点(QZ)、直缓点(ZH)、缓圆点(HY)、圆缓点(YH)、缓直点(HZ)位置如图5、图6、图7所示。󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮
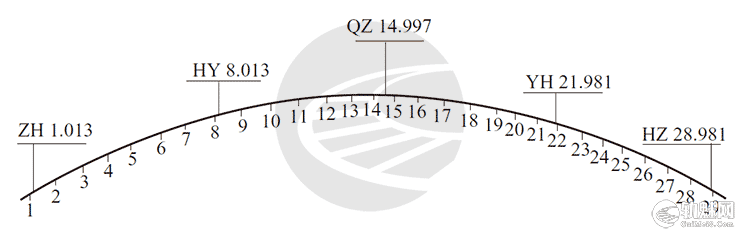
图5 曲线主要桩点位置
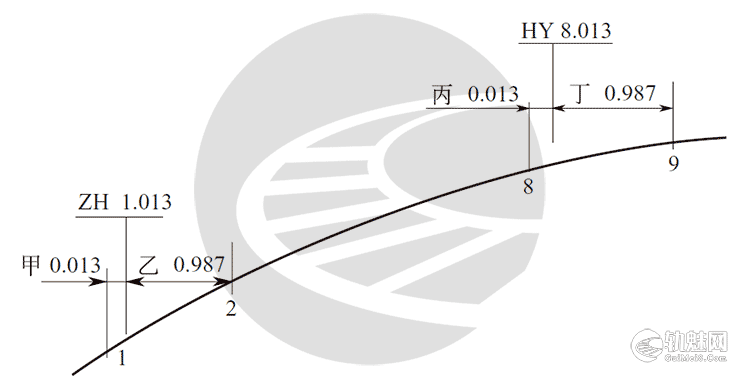
图6 缓和曲线始终点ZH、HY位置
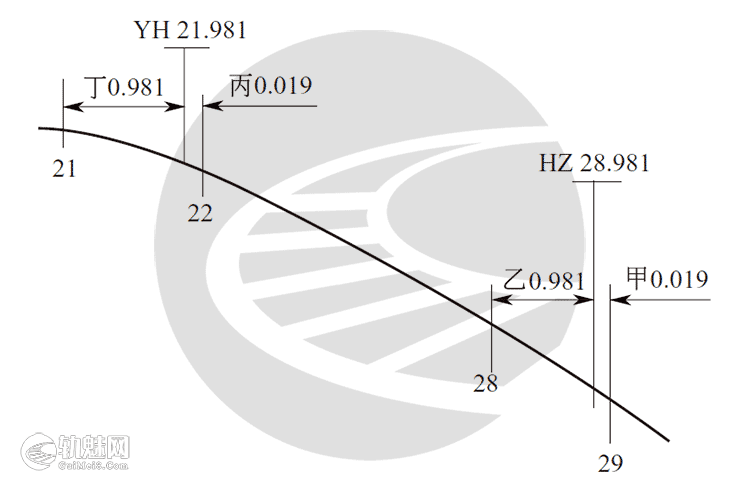
图7 缓和曲线始终点YH、HZ位置
[/login]
文章来源:
陈知辉 著《铁路曲线轨道(第2版)》2016年󠄐󠅅󠄹󠄴󠄪󠄾󠅟󠅤󠄐󠄼󠅟󠅗󠅙󠅞󠄬󠅒󠅢󠄟󠄮󠇘󠆭󠆘󠇙󠆝󠅵󠇗󠆭󠆁󠄐󠇗󠅹󠅸󠇖󠆍󠅳󠇖󠅹󠅰󠇖󠆌󠅹󠄬󠅒󠅢󠄟󠄮




学习了,好资料。